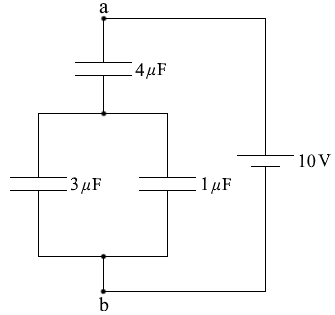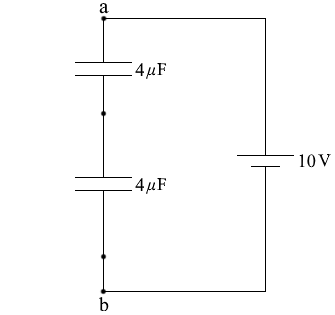
図1のように、電気容量がそれぞれ 4μF 、3μF 、1μF のコンデンサーC1、C2、C3 をつなぎ、端子a、bに 10V の直流電源をつないだ。このとき、コンデンサーC1、C2、C3 にそれぞれ蓄えられる電気量 Q1 、Q2 、Q3 の間の関係を表す式、および電気量 Q1 の値の組合せとして最も適当なものを、下の①〜⑨のうちから一つ選べ。ただし、電源を接続する前に各コンデンサーに電荷は蓄えられていなかった。
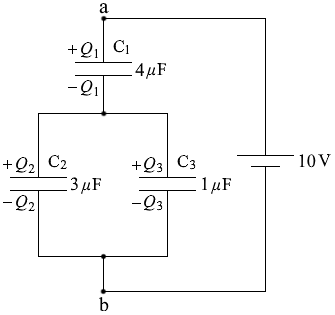
| 電気量の関係 | Q1 [C] | |
|---|---|---|
| ① | Q1 = Q2 + Q3 | 2×10-5 |
| ② | Q1 = Q2 + Q3 | 5×10-5 |
| ③ | Q1 = Q2 + Q3 | 8×10-5 |
| ④ | Q2 = Q3 + Q1 | 2×10-5 |
| ⑤ | Q2 = Q3 + Q1 | 5×10-5 |
| ⑥ | Q2 = Q3 + Q1 | 8×10-5 |
| ⑦ | Q3 = Q1 + Q2 | 2×10-5 |
| ⑧ | Q3 = Q1 + Q2 | 5×10-5 |
| ⑨ | Q3 = Q1 + Q2 | 8×10-5 |
#センター16本試物理
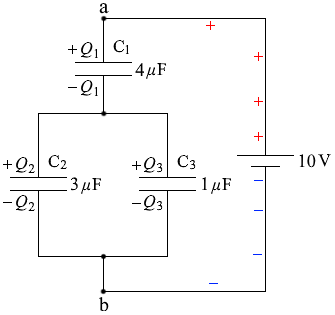電源を接続すると電荷が移動していくわけですが、
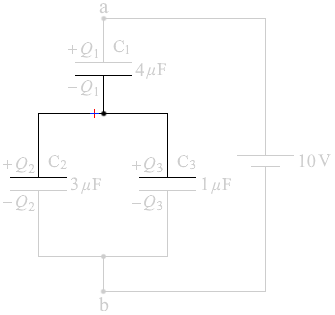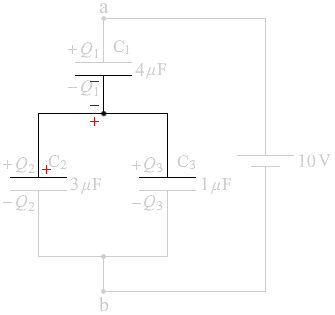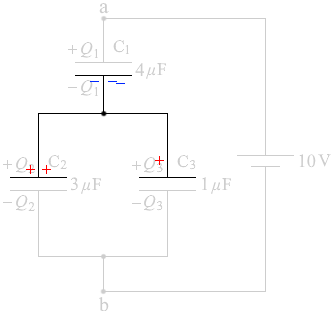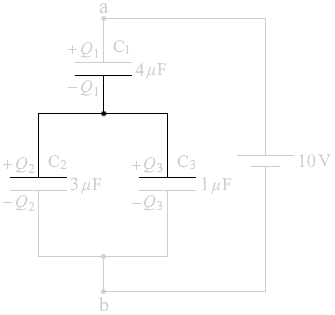このとき、左図の領域の部分にも電荷が発生します。
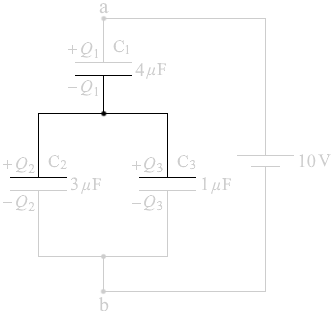この部分は独立した島であり、外部からの電荷の出入りは無く、この領域内で正電荷 
と負電荷 
の数は同数です。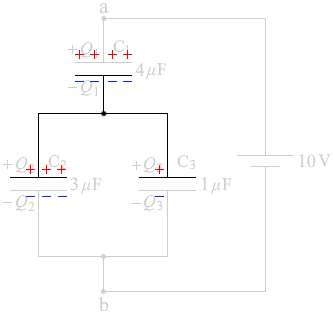
そして、コンデンサーの対面には必ず同数の異符号の電荷がいます。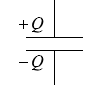
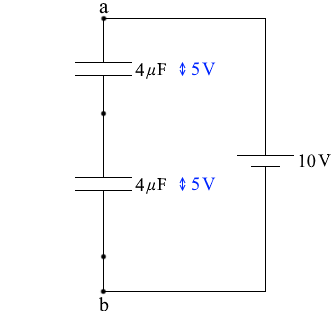コンデンサーに蓄えられる電気量（電荷）Qというのは
正極に +Q 、負極に -Q という意味です。
両方合わせて 2Q ということではありません。
これはつまり、
Q1 = Q2 + Q3
ということです。
さらに、
並列接続のコンデンサーの電気容量は単純に足すことができるので、4μF であり、
同じコンデンサーが2つ直列に並んでいるとみなすことができ、それぞれに掛かる電圧は 5V であると分かります。
つまり、コンデンサーC1には 5V の電圧が掛かり、電気量は電気容量と電圧を掛けたものだから、
Q1 = 4μ × 5 = 20μ = 20×10-6 = 2.0×10-5 [C]
答えは ① です。
（余談）
コンデンサーC2とC3の合成容量を C23 とすると、並列接続だから、
C23 = C2 + C3 = 3μ + 1μ = 4μ [F]
コンデンサーC1とC23の合成容量を C123 とすると、直列接続だから、
\(\large{\frac{1}{C_{123}}}\) = \(\large{\frac{1}{C_1}}\) + \(\large{\frac{1}{C_{23}}}\) = \(\large{\frac{1}{4μ}}\) + \(\large{\frac{1}{4μ}}\) = \(\large{\frac{1}{2μ}}\)
∴ C123 = 2μ [F]
これに 10V の電圧が掛かると考えれば、
Q1 = 2μ × 10 = 2.0×10-5 [C]
となります。