コンデンサー
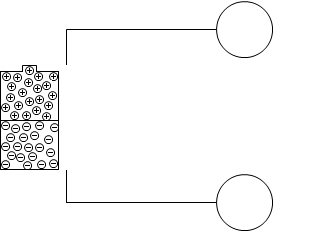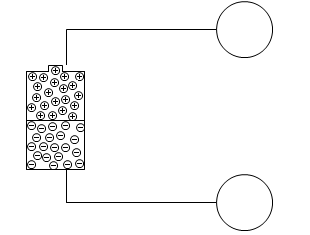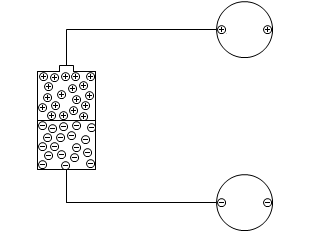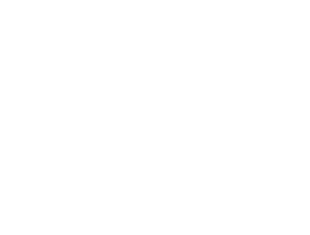導体Aに電池の＋極、導体Bに電池のー極をつなぐと、導体Aは正に帯電し、導体Bは負に帯電します。
導体Aと電池の＋極を領域Aとしますと、領域Aの中で正電荷が押し合いへし合いをして、その結果、導体Aに正電荷が現れます。押し合いへし合いは領域Aが等電位になるまで続き、等電位になったところで電荷の動きは止まります（一種のパスカルの原理）。一方、導体Bと電池のー極を領域Bとしますと、領域Bでも同様のことが起こり、導体Bに負電荷が現れます。
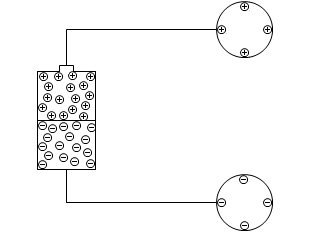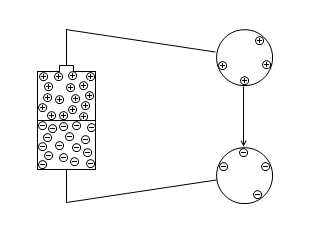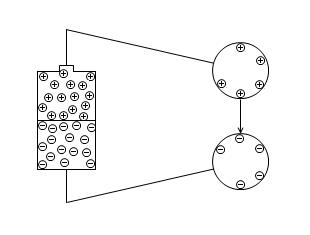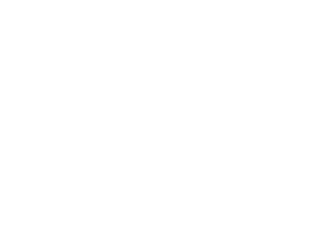次に、導体Aと導体Bを近づけると、それぞれの正電荷と負電荷が引きつけ合い、導体内に余白が生まれ、押し合いへし合いの末、余白に正電荷あるいは負電荷が割り込んで来ます。
つまり、導体Aと導体Bを近づけると、そこに溜まる電荷が増えるのです。
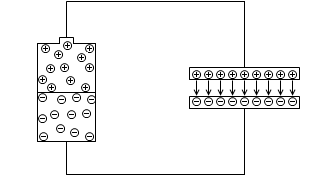なるべく多くの電荷を溜めたい場合は、導体の形を板状にして、大きくして、近づけるといいです。
このように電荷を溜めることができる装置をコンデンサーといいます。溜めるための導体を極板といいます。そして極板が平行なとき、これを平行板コンデンサーといいます。
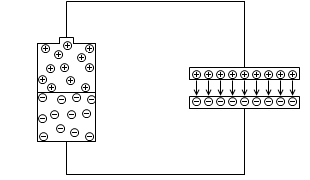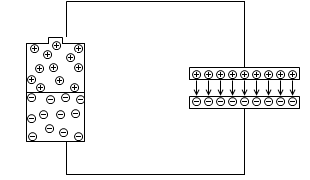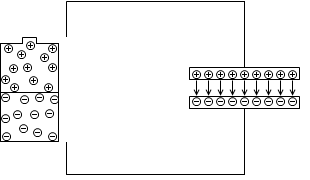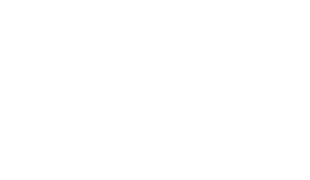一度コンデンサーに溜まった電荷は、電池を切り離しても、そのまま留まります。正電荷と負電荷がお互いに引きつけ合っているからです。
電気容量
蓄えられた電気量
コンデンサーの片方の極板に +Q [C] 、もう片方の極板に -Q [C] の電気量が帯電しているとき、このコンデンサーには Q [C] の電気量が蓄えられている、と定義します。（決して、合計で 0 になるなどと考えたり、絶対値を合計して 2Q になるなどと考えたりしません）
この、コンデンサーに蓄えられた電気量 Q [C] と、コンデンサーの極板間の電位差（電圧）V [V] の関係を探ってみます。
電気力線の本数
極板間の電場の強さを E [V/m] ＊[V/m] = [N/C]閉じるとし、1m2当たりの電気力線の本数を E 本とします。（普通、電気力線の密度は電場の強さと数値が同じになるように設定します。）
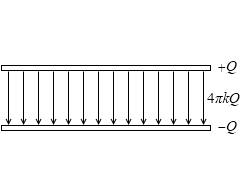すると、Q [C] の電荷が蓄えられたコンデンサーの極板間の電気力線の総数は、ガウスの法則より、4πkQ 本です。これは正極板から湧き出す電気力線がすべて負極板に向かうとみなしたときの考え方です。
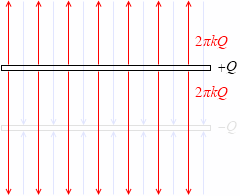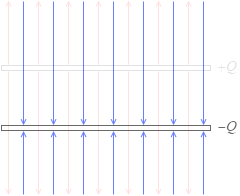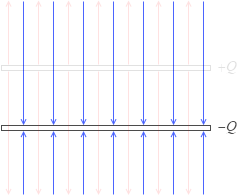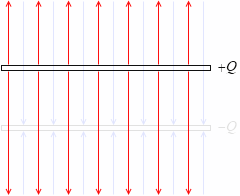電気力線を求める考え方は、もう一つあります。
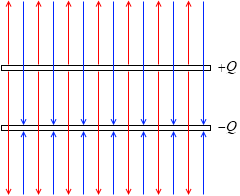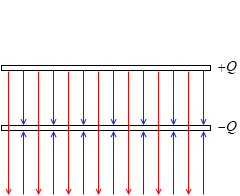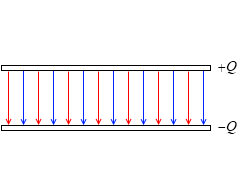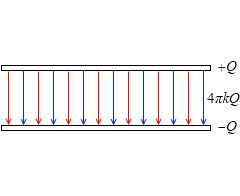
+Q [C] の電荷を蓄えた正極板からは、上にも下にも電気力線が湧き出ていて、その総数が 4πkQ 本であり、上へ 2πkQ 本、下へ 2πkQ 本湧き出しています。-Q [C] の電荷を蓄えた負極板は、上からも下からも電気力線を吸い込んでいて、その総数が 4πkQ 本であり、上から 2πkQ 本、下から 2πkQ 本吸い込んでいます。
正極板の上側は、それぞれの電気力線の方向が逆なので打ち消し合います。負極板の下側も、同様に打ち消し合います。残るのは極板間の電気力線だけで、それぞれの電気力線の方向が同じなので、電気力線の総数は 2πkQ 本の倍の 4πkQ 本となります。
このように、考え方には二通りあります。結果は同じですので、どちらの考え方でも構いません。
電気力線の本数のもう一つの表現方法
電気力線の本数に関しては、もう一つの表現方法があります。
コンデンサーの極板の形は正極板も負極板も同じで、面積が S [m2] であるとします。そうしますと、今、1m2当たりの電気力線の本数を E 本と決めているので、この極板から出る電気力線の本数は S×E = ES 本です。
つまり、このコンデンサーの極板間の電気力線の本数は 4πkQ 本であり、ES 本です。
4πkQ = ES ……①
回りくどい話になってしまって分かりにくいかもしれませんが、静電気の分野においては、このように架空の電気力線をイメージしながら物理量の関係式を導き出したりします。電荷から発生する静電気力の影響力というものは、正電荷から負電荷（負電荷が無い場合は無限遠の彼方）を結ぶ線、電気力線を仮定して、それをどのようにくるむか（ガウスの法則）、くるんだ領域の中に何本の電気力線があるか、ということを考えていきます。
電気量と電位差の関係
①式によって電気量 Q と電場 E の関係が分かりました。あとは電場 E と電位差 V との関係が分かれば、電気量 Q と電位差 V の関係が分かります。
平行板コンデンサーの極板間の電場は、あきらかに「一様」です。電気力線はまっすぐだし、等間隔です。となりますと、極板間の距離を d [m] としたとき、
V = Ed
が成り立ちます。変形しますと、
E = \(\large{\frac{V}{d}}\) ……②
②式を①式に代入しますと、
4πkQ = \(\large{\frac{V}{d}}\)S
∴ 4πkQ = \(\large{\frac{S}{d}}\)V
∴ Q = \(\large{\frac{1}{4\pi k}\frac{S}{d}}\)V ……③
これで電気量 Q と電位差 V の関係が導き出せました。
電気容量
③式の \(\large{\frac{1}{4\pi k}\frac{S}{d}}\) の部分は定数です。k はクーロンの法則の比例定数ですし、S はコンデンサーの極板の面積ですし、d は極板間の距離です。この定数の部分には意味があって、これを電気容量（静電容量、キャパシタンス＊capacitance = capacity（容量）+ ance（量・程度を表す名詞語尾）閉じる）と呼びます。量記号には C を用います。
単位は [F] ファラド ＊19世紀のイギリスの物理学者マイケル・ファラデーから。ファラデーの電磁誘導の法則を発見した人です。
昔使われていた [Fd] ファラデー という電荷の単位もこの人にちなんでいます。
閉じるです。上式より [C] = [F]×[V] ですので [V] = [C/F] でもあります。この [F] はちょっと大きすぎる単位で、実際には [μF] マイクロファラド ＊=10-6 F閉じるや [pF] ピコファラド ＊=10-12 F閉じるがよく用いられます。
上式より、コンデンサーに蓄えられる電気量 Q は、電気容量 C と極板間の電位差 V に比例します。電位差が同じであれば電気容量が大きいほど多くの電気量が溜められます。電気容量はコンデンサーの電荷の溜めやすさを表している、といえます。
さらに、
C = \(\large{\frac{1}{4\pi k}\frac{S}{d}}\)
とおきましたので、電気容量 C は極板の面積 S に比例し、極板間 d に反比例する、といえます。コンデンサーは、極板が大きいほど、また、極板間が小さいほど電荷がたくさん溜まるということです。
さらに、\(\large{\frac{1}{4\pi k}}\) を ε とおくと、
C = ε\(\large{\frac{S}{d}}\)
となります。ε を誘電率といいます。
話の流れ
上の①式からの流れをまとめてみます。
4πkQ = ES ……①
E = \(\large{\frac{V}{d}}\) ……②
Q = \(\underbrace{\underbrace{\large{\frac{1}{4\pi k}}}_{ε}\large{\frac{S}{d}}}_{C}\)V ……③