コンデンサーの接続

複数のコンデンサーをつなげる

複数のコンデンサーをつなげるとき、つなげ方によってコンデンサーの性能が上がるのか下がるのか考えてみます。

『直列接続と並列接続』項において、導線の電気抵抗は、直列に接続したときと並列に接続したときで違いが出ることを説明しましたが、それと似たような話です。

コンデンサーの並列接続

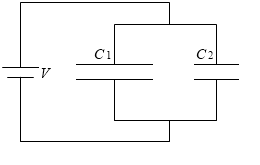左図のように、電気容量が C₁ [F] と C₂ [F] のコンデンサーを並列につなぎ、それを電圧 V [V] の電池につないで２つのコンデンサーを充電します。

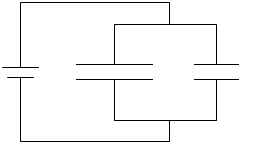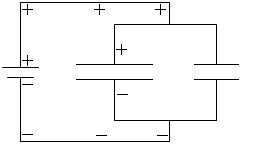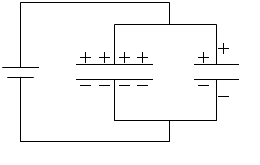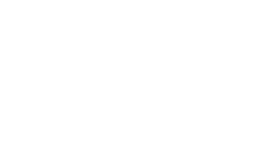充電は左図のAの領域が等電位、Bの領域が等電位になるまで続きます。充電が終わると２つのコンデンサーのそれぞれの電圧は V になります。

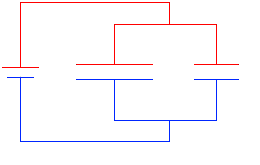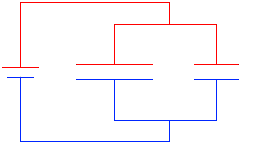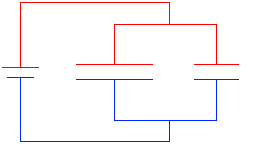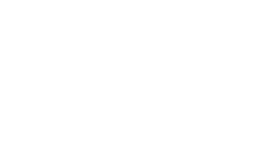領域A内が等電位で、領域B内が等電位で、領域Aと領域Bの電位差が（電池の部分で）V であるならば、領域Aと領域Bはどの地点とどの地点をとっても電位差が V です。

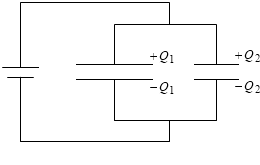それぞれのコンデンサーに蓄えられる電荷を Q₁ [C] 、Q₂ [C] とすると、

　　　　Q₁ = C₁V
　　　　Q₂ = C₂V

となります。そうしますと２つのコンデンサーの全体の電荷 Q [C] は、

　　　　Q = Q₁ + Q₂ = C₁V + C₂V = (C₁ + C₂)V

となります。(C₁ + C₂) は２つのコンデンサーを１つの大きなコンデンサーと考えたときの電気容量とみなすことができます。この電気容量を合成容量といいます。これを C [F] とおきますと、

となります。これは３つ以上のときでも成り立ちます。

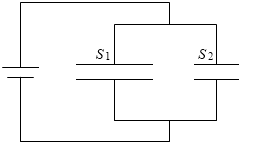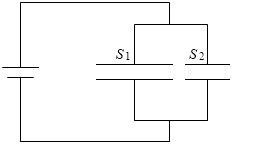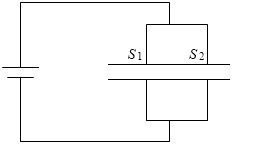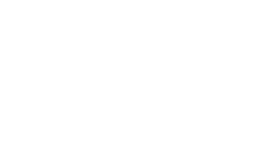この法則からいえることは、複数のコンデンサーを並列に接続するということは、コンデンサーの極板の面積を大きくすることと同じであるということです。

C₁ のコンデンサーの極板の面積を S₁ 、C₂ のコンデンサーの極板の面積を S₂ とし、どちらのコンデンサーも誘電率が ε 、極板間が d で同じとしますと、

　　　　C₁ = ε\(\large{\frac{S_1}{d}}\)

　　　　C₂ = ε\(\large{\frac{S_2}{d}}\)

ですので、上の法則より、

　　　　C = C₁ + C₂ = ε\(\large{\frac{S_1}{d}}\) + ε\(\large{\frac{S_2}{d}}\) = ε\(\large{\frac{(S_1+S_2)}{d}}\)

となり、誘電率と極板間の大きさが共通しているコンデンサーの並列接続は、単に極板面積を広げた (S₁+S₂) のと同等、といえます。

コンデンサーの直列接続

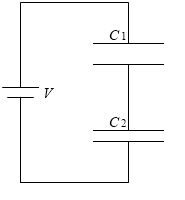左図のように、電気容量が C₁ [F] と C₂ [F] の未充電＊以下導き出す式は、未充電の状態から充電していった場合の話です。もし、始めに充電されているとかなりややこしい話になります。

並列接続の場合はこのことにこだわる必要はありません。どっちみちすべてのコンデンサーは電源と同じ電圧になります。
　閉じるのコンデンサーを直列につなぎ、それを電圧 V [V] の電池につないで２つのコンデンサーを充電します。

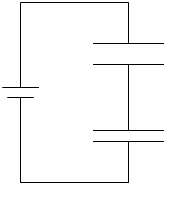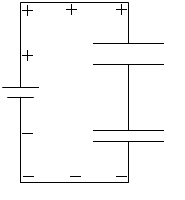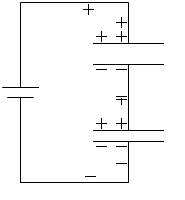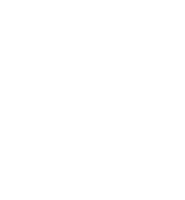すると C₁ のコンデンサーの正極板にたどりついた正電荷は対面の極板の負電荷をおびき寄せます。静電誘導です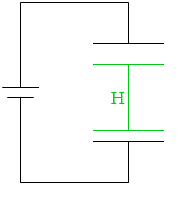＊誘電分極ではありません。静電誘導と誘電分極の区別はつきますでしょうか。今の場合、H の領域の物質は”導体”で、静電誘導が起きています。
　閉じる。C₂ のコンデンサーの負極板にたどりついた負電荷は対面の極板の正電荷をおびき寄せます。

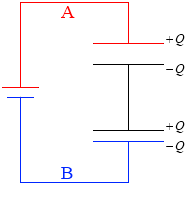充電は左図のAの領域が等電位、Bの領域が等電位になるまで続きます。等電位になったときの C₁ のコンデンサーの正極板に溜まった電荷を +Q [C] とすると、その負極板には -Q [C] の電荷、C₂ のコンデンサーの正極板には +Q [C] 、負極板には -Q [C] の電荷が溜まります。

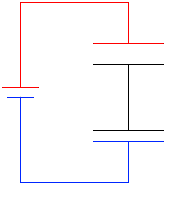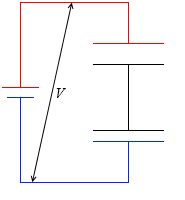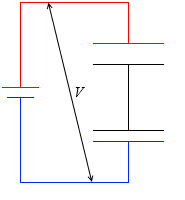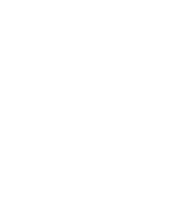充電が終わったとき、領域A内は等電位で、領域B内も等電位で、領域Aと領域Bはどの地点とどの地点をとっても電位差が V です。

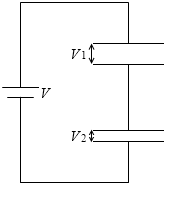このときの C₁ のコンデンサーの極板間の電位差を V₁ [V]、C₂ のコンデンサーの極板間の電位差を V₂ [V] としますと、

　　　　V₁ = \(\large{\frac{Q}{C_1}}\)

　　　　V₂ = \(\large{\frac{Q}{C_2}}\)

であり、　V = V₁ + V₂　であるので、

　　　　V = V₁ + V₂ = \(\large{\frac{Q}{C_1}}\) + \(\large{\frac{Q}{C_2}}\) = (\(\large{\frac{1}{C_1}}\) + \(\large{\frac{1}{C_2}}\))Q

となります。そして、２つのコンデンサーを１つの大きなコンデンサーとみなしたときの合成容量を C [F] とすれば、

　　　　V = \(\large{\frac{1}{C}}\)Q

ですので、上式と見比べると、

　　　　\(\large{\frac{1}{C}}\) = (\(\large{\frac{1}{C_1}}\) + \(\large{\frac{1}{C_2}}\))

となっています。

これは３つ以上のときでも成り立ちます。

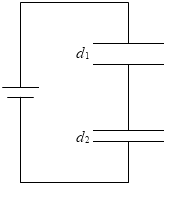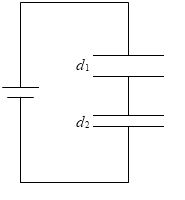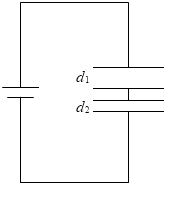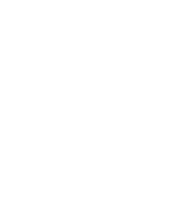この法則からいえることは、複数のコンデンサーを直列に接続するということは、コンデンサーの極板間を大きくすることと同じということです。

C₁ のコンデンサーの極板間の大きさを d₁ 、C₂ のコンデンサーの極板間の大きさを d₂ とし、どちらのコンデンサーも誘電率が ε 、極板の面積が S で同じとしますと、

　　　　C₁ = ε\(\large{\frac{S}{\ d_1}}\)

　　　　C₂ = ε\(\large{\frac{S}{\ d_2}}\)

ですので、上の法則より、

　　　　\(\large{\frac{1}{C}}\) = \(\large{\frac{1}{C_1}}\) + \(\large{\frac{1}{C_2}}\) = \(\large{\frac{\ d_1}{εS}}\) + \(\large{\frac{\ d_2}{εS}}\) = \(\large{\frac{(d_1+d_2)}{εS}}\)

　∴　　C = \(\large{\frac{εS}{(d_1+d_2)}}\) = ε\(\large{\frac{S}{(d_1+d_2)}}\)

となり、誘電率と極板の面積が共通しているコンデンサーの直列接続は、単に極板間を大きくした (d₁+d₂) のと同等、といえます。＊コンデンサーの性能は極板間 d の大きさに反比例します。コンデンサーは直列に接続すると性能が落ちるということです。１つ１つに掛かる電圧を抑えることができますが。
　閉じる

まとめ

以上まとめますと、

コンデンサーは、
並列に接続すると容量が増え、電荷をたくさん溜めることができ、
直列に接続すると容量は減り、電荷はあまり溜めることができないが、１つ１つに掛かる電圧を抑えることができる、

となります。

電気抵抗のときと逆

『直列接続と並列接続』項は電気抵抗の接続の話でしたが、そのときは、直列接続のときが単純な和で、並列接続のときが逆数の和、でした。

本項では逆で、並列接続のときが単純な和で、直列接続のときが逆数の和、です。

ばねの接続でも、並列接続のときが単純な和で、直列接続のときが逆数の和、でした。

ちなみに、電池に関しては、直列に接続すると電圧を上げることができ、並列に接続すると電圧は変わらないが長持ちさせることができます。小学校の理科で習ったと思います。