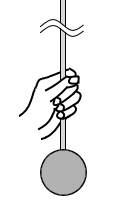
質量 0.50 kg のおもりに軽くて細い棒をつけ、図2のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少しゆるめ、摩擦力を一定に保ちながらおもりに等加速度運動をさせたところ、はじめの 1.0 秒間に 0.50 m 降下した。ただし、重力加速度を 9.8 m/s2 とする。
(問1)おもりの加速度の大きさはいくらか。
(問2)0.50 m 降下したときのおもりの速さはいくらか。
(問3)qG7FJ
#センター97本試
質量 0.50 kg のおもりに軽くて細い棒をつけ、図2のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少しゆるめ、摩擦力を一定に保ちながらおもりに等加速度運動をさせたところ、はじめの 1.0 秒間に 0.50 m 降下した。ただし、重力加速度を 9.8 m/s2 とする。

(問1)おもりの加速度の大きさはいくらか。
(問2)0.50 m 降下したときのおもりの速さはいくらか。
(問3)qG7FJ
#センター97本試
(問1)
求める加速度の大きさを a [m/s2] としますと、等加速度直線運動の変位の関係式( x = v0t + \(\large{\frac{1}{2}}\)at2 )より、
0.50 = 0×1.0 + \(\large{\frac{1}{2}}\)×a×1.02
∴ 0.50 = \(\large{\frac{1}{2}}\)×a×1.02
∴ 1.0 = a×1.02
∴ a = 1.0 [m/s2]
(問2)
求める速度の大きさを v [m/s] としますと、0.50 m 降下したとき時間は 1.0 秒経っているから、等加速度直線運動の速度の関係式( v = v0 + at )より、
v = 0 + 1.0×1.0
∴ v = 1.0 [m/s]
(あるいは等加速度直線運動の t を含まない関係式( v2 - v02 = 2ax )を立てて、v2 - 02 = 2×1.0×0.50 としても求まります。)