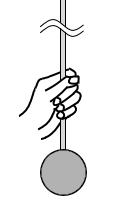
質量 0.50 kg のおもりに軽くて細い棒をつけ、図2のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少しゆるめ、摩擦力を一定に保ちながらおもりに等加速度運動をさせたところ、はじめの 1.0 秒間に 0.50 m 降下した。ただし、重力加速度を 9.8 m/s2 とする。
(問1)
(問2)qG7FI
(問3)おもりが 0.50 m 降下したはじめの 1.0 秒間に手と棒の間で発生した熱量は、位置エネルギーの変化量のほぼ何%に当たるか。
#センター97本試
質量 0.50 kg のおもりに軽くて細い棒をつけ、図2のように棒のおもりに近い部分を手でつかんで静止させる。手の位置は変えずに力を少しゆるめ、摩擦力を一定に保ちながらおもりに等加速度運動をさせたところ、はじめの 1.0 秒間に 0.50 m 降下した。ただし、重力加速度を 9.8 m/s2 とする。

(問1)
(問2)qG7FI
(問3)おもりが 0.50 m 降下したはじめの 1.0 秒間に手と棒の間で発生した熱量は、位置エネルギーの変化量のほぼ何%に当たるか。
#センター97本試
位置エネルギーの変化量を ΔU [J] と置きますと、
ΔU = ( mgh ) = 0.50×9.8×0.50 = \(\large{\frac{1}{2}}\)×9.8×\(\large{\frac{1}{2}}\) = 2.45 [J]
これは位置エネルギーの変化量であると同時に、手を使ってない場合の運動エネルギーの増加分でもあるはずです。
運動エネルギーの増加分を ΔK [J] と置きますと、
スタート時の運動エネルギー:( \(\large{\frac{1}{2}}\)mv2 ) = \(\large{\frac{1}{2}}\)×0.50×02 = 0 [J]
1.0秒後の運動エネルギー:( \(\large{\frac{1}{2}}\)mv2 ) = \(\large{\frac{1}{2}}\)×0.50×1.02 = 0.25 [J] (∵ qG7FIの問2より v = 1.0 [m/s])
∴ ΔK = 0.25 [J]
2.45 [J] 増えるはずが 0.25 [J] しか増えなかったということです。残りの 2.20 [J] は摩擦熱(熱量)になったということです。
つまり、求める割合は
\(\large{\frac{2.20}{位置エネルギーの変化量ΔU}}\)×100 = \(\large{\frac{2.20}{2.45}}\)×100 ≒ 0.898×100 ≒ 90 [%]
(余談)
手を使わず自由落下させた場合には、0.50m 落ちたときの速度は、(t を含まない式 v2 = 2gy を立てて)
v2 = 2×9.8×0.50
∴ v = \(\sqrt{9.8}\) ≒ 3.13 [m/s]
0.50m 落ちる時間は、(変位の関係式 y = \(\large{\frac{1}{2}}\)gt2 を立てて)
0.50 = \(\large{\frac{1}{2}}\)×9.8×t2
∴ t = \(\sqrt{\frac{1}{9.8}}\) ≒ 0.319 [s]
0.50m 落ちたときの運動エネルギーは
( \(\large{\frac{1}{2}}\)mv2 ) = \(\large{\frac{1}{2}}\)×0.50×(\(\sqrt{9.8}\))2 = \(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)×9.8 = 2.45 [J]
となり、上で示した位置エネルギーの変化量 ΔU = 2.45 [J] に一致します。