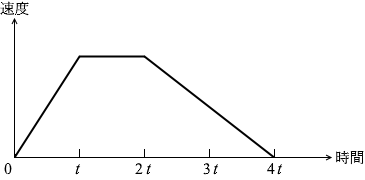
速度と時間のグラフ(v -t グラフ)の曲線とt 軸に挟まれる部分の面積が変位(移動距離)である から、
この台形の高さは、t だけ時間が経ったときの速度です。この間、0 の速度でスタートして、a の加速度で等加速度運動をしていますので、この速度は at です 。
*
左図は上昇した後、下降したというグラフではないので勘違いしないでください。閉じる
台形の面積は (上底+下底)×高さ÷2 ですから、
( t + 4t ) × at ÷ 2 = \(\large{\frac{5}{2}}\)at 2
です。
(別解:v -t グラフの面積が変位、ということを忘れてしまった場合には)等加速度直線運動 の変位の式( x = v 0 t + \(\large{\frac{1}{2}}\)at 2 )を使って求めていきます。
(0 から t までは)h 1 = 0×t + \(\large{\frac{1}{2}}\)at 2
= \(\large{\frac{1}{2}}\)at 2
(t から 2t までは)h 2 = at ×t + \(\large{\frac{1}{2}}\)×0×t 2
= at 2
(2t から 4t までは)h 3 = at ×2t + \(\large{\frac{1}{2}}\)×(-\(\large{\frac{1}{2}}\)a )×(2t )2 ∵グラフから読み取ると加速度は -\(\large{\frac{1}{2}}\)a
= 2at 2 - at 2
= at 2
(合計は)h 1 + h 2 + h 3 = \(\large{\frac{1}{2}}\)at 2 + at 2 + at 2
= \(\large{\frac{5}{2}}\)at 2
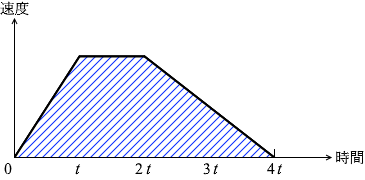 左図の台形部分の面積が求める距離です。
左図の台形部分の面積が求める距離です。