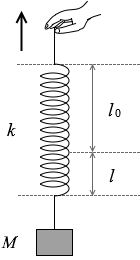
ばね定数 k 、自然の長さ l0 のばねがある。図6のように、質量 M のおもりをばねの一端に取り付け、他端を持って引き上げた。ばねの伸びが l であるとき、おもりの加速度はいくらか。ただし、加速度の正の向きは鉛直上向きとし、重力加速度の大きさを g とする。また、ばねの質量は無視できるものとする。
#センター07本試
ばね定数 k 、自然の長さ l0 のばねがある。図6のように、質量 M のおもりをばねの一端に取り付け、他端を持って引き上げた。ばねの伸びが l であるとき、おもりの加速度はいくらか。ただし、加速度の正の向きは鉛直上向きとし、重力加速度の大きさを g とする。また、ばねの質量は無視できるものとする。
#センター07本試
（おもりにはたらく力を割り出して運動方程式を立てる）
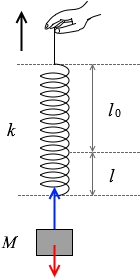ばねが l だけ伸びているので、ばねが引っ張る力は kl です。これは手の力でもあります。
重力は下向きに Mg で引っ張っています。
よって、おもりの加速度を a とすると、おもりの運動方程式は
Ma = kl - Mg
となり、
a = \(\large{\frac{kl}{M}}\) - g
と分かります。
この問題は静止してないので力のつり合いの問題ではありません。あくまでも動いている最中の話です。エレベーターで上へ加速しているような場面です。エレベーターでは力の大きさが分かりませんが、この場合はばねを使っているので力の大きさが分かります。ばねばかりを使っていることと同じです。ばねばかりが用いられていれば手がどれだけ力を入れたのかが特定できます。距離や時間を測らなくても加速度を導き出せます。
上に持ち上げてから徐々に手の力を弱めていくとやがて等速になります。
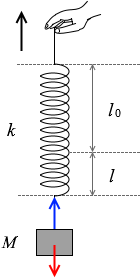kl と Mg が等しくなった状態です。
計算すると、
kl = Mg
∴ l = \(\large{\frac{M}{k}}\)g
と分かります。これは普通に天井から下げられたばねに物体をつるした場合と同じ伸びです。
この値を a = \(\large{\frac{kl}{M}}\) - g に代入すればちゃんと a = 0 となります。加速度が 0、すなわち等速です。