同じ質量 M の二つの物体A、Bが軽い糸で結ばれており、糸は、天井に固定されたなめらかに回る軽い滑車にかけられている。Aの上には中央に穴の開いた質量 m の物体Cがのっている。Aの下側には穴の開いた固定台があり、Aはこの台に接触せず、穴を通り抜けるようになっている。
図1(a)のように、Bを手で静止させ、時刻 t=0 でBを静かに放すと、AとCは一体となって落下しはじめた。Aの上面が固定台の上面に達したとき、Cが固定台によって取り除かれた。この時刻を t=t0 とする。図1(b)は時刻 t > t0 の様子を表す。ただし、糸とCは接触することはないものとする。また、重力加速度の大きさを g とする。
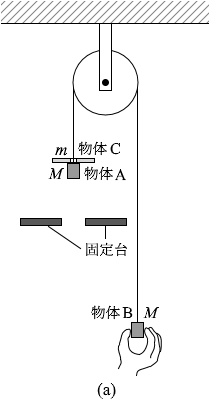
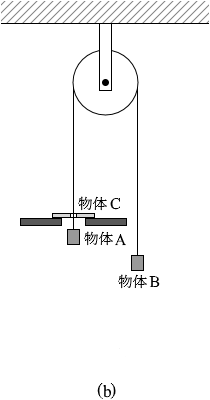
（問1）物体AとCが落下しはじめてからAの上面が固定台の上面に達するまでの運動を考える。物体Aの加速度の大きさを式で表わせ。
（問2）物体Aの速さと時刻の関係を表すグラフとして最も適当なものを、次の①～④のうちから一つ選べ。
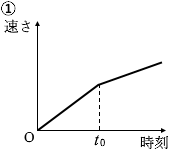
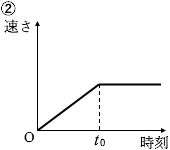
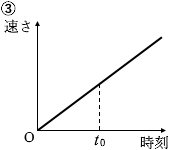
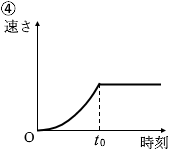
#センター14本試
（問1）
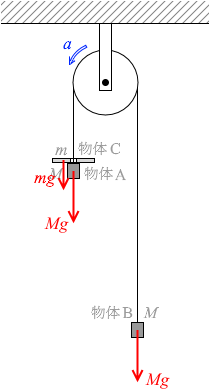この運動の最中に糸がたるむことはないので、物体A、B、Cを一つの物体とみなし、求める加速度を a と置いて運動方程式（ ma=F ）を立てますと、
(M + m + M)a = Mg + mg - Mg ……➊
∴ (2M + m)a = mg
∴ a = \(\large{\frac{mg}{2M+m}}\)
（別解）
張力を T と置いて、
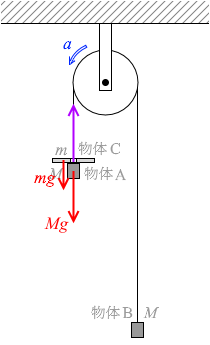物体A、Cについての運動方程式を立てますと、
(M + m)a = Mg + mg - T ……➋
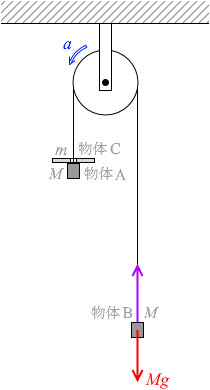物体Bについての運動方程式を立てますと、
Ma = - Mg + T ……❸
➋式と❸式を足し合わせますと、
(M + m + M)a = Mg + mg - Mg
➊式と同じになります。
（問2）
a = \(\large{\frac{mg}{2M+m}}\)
という値は定数であり、一定です。つまり、t=t0 までは等加速度直線運動です。速度と時間の式（v = v0 + at）を立てますと、
v = \(\large{\frac{mg}{2M+m}}\)t
です。v は t によって直線的に増えていきます。（もし v = \(\large{\frac{mg}{2M+m}}\)t2 となっていたりすれば v-tグラフの曲線は放物線となります）
t > t0 においては、
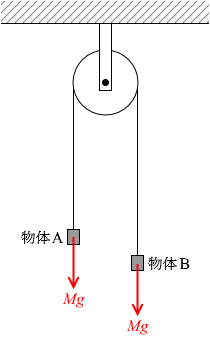物体Aにはたらく Mg の力と物体Bにはたらく Mg の力がつり合い、物体の運動は変化しなくなります。慣性の法則です。外力の総計が 0 なので加速も減速もしません。t=t0 における速度がそのまま保たれます。
このようなことを表しているグラフは ② です。