滑車につるされた2物体
前提
滑車に吊るされた2物体の運動について考えます。
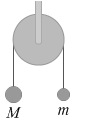 物体の質量はそれぞれ M、m(M > m)で、滑車は天井に固定されていて、なめらかに回り、質量が無く、糸にも質量が無いとします。重力加速度の大きさを g とします。
物体の質量はそれぞれ M、m(M > m)で、滑車は天井に固定されていて、なめらかに回り、質量が無く、糸にも質量が無いとします。重力加速度の大きさを g とします。
滑車がなめらかに回るということは、摩擦が無く、物体の動きにブレーキを掛けるようなことが無いということです。運動方程式 m a = F の F に影響を与えないということです。
それから、滑車にも糸にも質量が無いということは、これも物体の動きにブレーキをかけることが無いということです。質量があると、物体の運動の法則に影響を与えてしまいます。運動方程式 m a = F の質量 m の部分に滑車や糸の質量を組み込まなければならなくなってしまいます。高校物理の問題では、何もことわりがなければこのようなことが前提となっています。
もう一つ、糸の振る舞いの特徴として、糸の張力というものは糸のどの部分においても同じ大きさの力がはたらきます。そして力の方向は常に糸を引っ張るような方向にはたらきます。糸を圧縮するような方向には力ははたらきません。糸やひもやロープは常に引っ張る方向だけに力がはたらきます。さらに、それらが緩んだときというのは力がはたらいていないときです。これらが張力の特徴です。
運動方程式を立てる
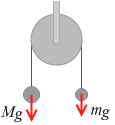 2物体をひとまとめにして、加速度を a として運動方程式を立ててみます*
2物体をひとまとめにして、加速度を a として運動方程式を立ててみます*
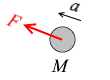 M [kg] の物体が F [N] で引っ張られて a [m/s2] で動くときの運動方程式は
M [kg] の物体が F [N] で引っ張られて a [m/s2] で動くときの運動方程式は
Ma = F
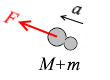 M + m [kg] の物体が F [N] で引っ張られて a [m/s2] で動くときの運動方程式は
M + m [kg] の物体が F [N] で引っ張られて a [m/s2] で動くときの運動方程式は
(M + m) a = F
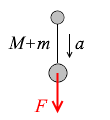 同じく
同じく
(M + m) a = F
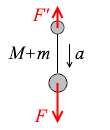 F - F' [N] で引っ張られるなら
F - F' [N] で引っ張られるなら
(M + m) a = F - F'
 同様にして
同様にして
(M + m) a = F - F'
で、このとき F - F' = Mg - mg なので書き直すと
(M + m) a = Mg - mg
閉じる。軽い方の物体は落下を妨げる方向に力がはたらくことに注意しますと、
(M + m) a = M g - m g
∴ (M + m) a = (M - m) g
∴ a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g
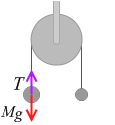 張力を T とおきますと、重い方の物体だけに着目したときの運動方程式は、
張力を T とおきますと、重い方の物体だけに着目したときの運動方程式は、
M a = M g - T
∴ T = M g - M a これに a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g を代入すると
= M g - M \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g
= \(\large{\frac{M(M+m)-M(M-m)}{M+m}}\) g
= \(\large{\frac{Mm+Mm}{M+m}}\) g
= \(\large{\frac{2Mm}{M+m}}\) g ……①
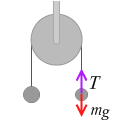 軽い方の物体だけに着目したときの運動方程式は、加速度は鉛直上向きであることに注意して、
軽い方の物体だけに着目したときの運動方程式は、加速度は鉛直上向きであることに注意して、
(ちなみに、張力 T が共通なのは力がつり合っているからではなく作用⋅反作用の法則のためです。今は加速している最中です。静止していません)
m a = T - m g
(鉛直下向きを正と定めて m(- a) = m g - T と立式してもいいです)
∴ T = m g + m a これに a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g を代入すると
= m g + m \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g
= \(\large{\frac{m(M+m)+m(M-m)}{M+m}}\) g
= \(\large{\frac{Mm+Mm}{M+m}}\) g
= \(\large{\frac{2Mm}{M+m}}\) g ……②
当然ですが、①式と②式は同一です。
3つの運動方程式を立てましたが、
全体 : (M + m) a = M g - m g
重い方 : M a = M g - T
軽い方 : m a = T - m g
この内のどれか2つを使って計算すると T が求められます。どの組合せを選んでもいいです。
解釈
a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g の式を解釈しますと、
いま M > m だから、加速度 a は常に正。
そして、M = m のとき a = 0 、つまり物体は動きません。
さらに、m = 0 のとき a = g 。M が自由落下していきます。
T = \(\large{\frac{2Mm}{M+m}}\) g の式を解釈しますと、
T は m g より大きく M g より小さいです。
このことを m < M を変形することによって証明してみます。
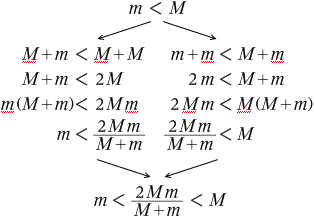
つまり、加速中の糸の張力というのは、一方の端が引っ張られる力より大きく、もう一方の端が引っ張られる力より小さい、ということです。この話は『接する物体』において F より f の方が小さい(力が目減りする)ことと通じるものがあります。
そして、張力 T = \(\large{\frac{2Mm}{M+m}}\) g がちょうど Mg または mg になるときというのは、M = m のときです。このとき a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g = 0 で物体は動かず、力がつり合っているときです。
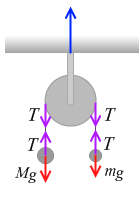 さらに、天井が滑車を支える力を考えてみますと、それは 2T です。すなわち 2T = \(\large{\frac{4Mm}{M+m}}\) g です。*上で説明しましたが、このとき、各地点の T の大きさは全て同じです。
さらに、天井が滑車を支える力を考えてみますと、それは 2T です。すなわち 2T = \(\large{\frac{4Mm}{M+m}}\) g です。*上で説明しましたが、このとき、各地点の T の大きさは全て同じです。
閉じる
Mg + mg ではありません。Mg + mg となるのは物体が加速していない場合です*加速していない場合というのは a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g = 0 ということであり、これはつまり、M = m のときです。
閉じる。物体が加速しているときは力のつり合いは成り立たちません。全重量が天井に掛かるわけではありません。これは勘違いしやすいポイントなので覚えておいてください。
\(\large{\frac{4Mm}{M+m}}\) g は Mg + mg より常に小さいです。
このことをまた m < M を変形することによって証明してみます。
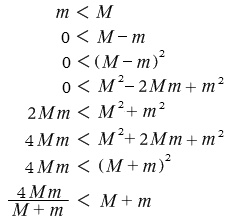
というわけで \(\large{\frac{4Mm}{M+m}}\) g は Mg + mg より小さいです。加速中は全重量が天井に掛かるわけではないのです。
全重量が掛かるときというのは加速しないときであり、それは a = \(\bigl(\large{\frac{M-m}{M+m}}\bigr)\) g = 0 ということであり、これはつまり、M = m ということであり、これは単に M の物体が2つ吊り下がっている、という状態です。
また、m が非常に小さいときは \(\large{\frac{4Mm}{M+m}}\) g も非常に小さくなり、これはつまり、天井にほとんど力が掛からないということです。重い方の物体は天井に負荷を掛けずにするすると糸が切れたように落下していきます。
アトウッドの器械
本項で示したような、滑車に2つの物体を吊るした装置をアトウッドの器械といいます。18世紀のイギリスの物理学者のアトウッドはこの装置を使って重力加速度を調べました。物体をそのまま単純に落として重力加速度を測定するより、この器械で加速度を小さくしてやった方が測定が容易になります。