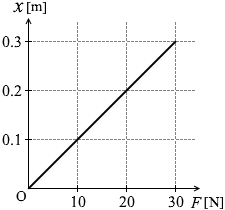
ばね定数 k の軽いばねの一端を固定し、他端を大きさ F の力で引っ張ったところ、図1のような、F と自然の長さからの伸び x の関係が得られた。x = 0.20 m のとき、ばねに蓄えられた弾性エネルギーは何Jか。
#センター17本試物理基礎
ばね定数 k の軽いばねの一端を固定し、他端を大きさ F の力で引っ張ったところ、図1のような、F と自然の長さからの伸び x の関係が得られた。x = 0.20 m のとき、ばねに蓄えられた弾性エネルギーは何Jか。
#センター17本試物理基礎
グラフを読み取りますと、伸び x = 0.10 [m] のときの力が F = 10 [N] だから、これらの数値をフックの法則の式（F = kx）に代入して、ばね定数 k を求めますと、
10 = k × 0.1
∴ k = 100
次に、弾性エネルギーの式（U = \(\large{\frac{1}{2}}\)kx2）に k = 100 、x = 0.20 を代入しますと、
U = \(\large{\frac{1}{2}}\) × 100 × 0.202 = 100 × 0.10 × 0.20 = 2.0 [J]
（グラフがアブノーマル）
フックの法則を表すグラフは通常、横軸が x で縦軸が F ですが、図1は逆になってます。「弾性エネルギーの大きさは曲線と横軸で囲まれた面積」と覚えている人は
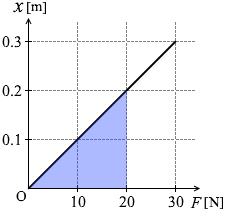この部分の面積を割り出そうとしてしまうかもしれませんが、
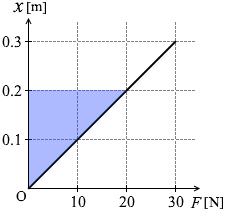本当は、
この部分の面積です。
しかし、どちらも同じ大きさなので正解を得られます。