箱の中に砂を質量 M だけ入れ、壁との間をばね定数 k のばねでつないだ。箱をつかみ、ばねを自然長から l だけ引き伸ばして静かに手を離したところ。図1のように箱は静止したままであった。ただし、床と箱との間の静止摩擦係数 μ 、動摩擦係数 μ' は場所によらず一定であり、重力加速度の大きさを g とする。また、箱とばねの質量は無視できるものとする。
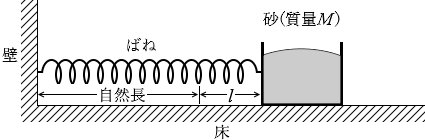
（問1）図1の状態で、床が箱に対して及ぼす力の方向はどうなるか。最も適当なものを、次の①～⑥のうちから一つ選べ。
（問2）箱の中の砂を少しずつ取り除く。砂を質量 m だけ取り除いたとき、箱が動き始めた。m はいくらか。
（問3）qG7F6
#センター04追試
（問1）図1の状態で、床が箱に対して及ぼす力の方向はどうなるか。最も適当なものを、次の①～⑥のうちから一つ選べ。
この場面で登場する力は以下の4つです。
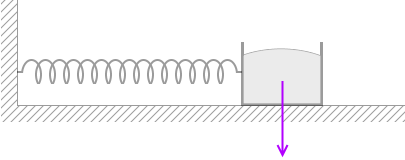㋐：砂の重力
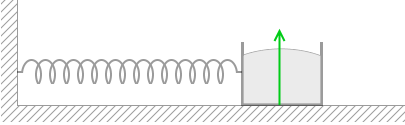㋑：垂直抗力
㋒：ばねの弾性力
㋓：静止摩擦力
このうち、「箱が床に対して及ぼす力」といえるのは㋑と㋓で、その合力はとしては ① が適しています。
（問2）箱の中の砂を少しずつ取り除く。砂を質量 m だけ取り除いたとき、箱が動き始めた。m はいくらか。
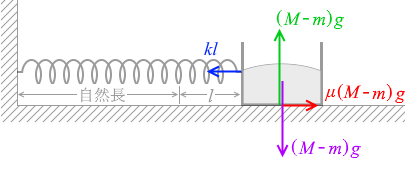m だけ取り除いたのだから砂の重力は (M - m)g 。
それに対抗する垂直抗力も (M - m)g 。
動き出す直前（=動き出す瞬間）の摩擦力は最大静止摩擦力であり、μ(M - m)g 。動き出す直前はこの摩擦力がばねの弾性力 kl とつり合っているのだから、
μ(M - m)g = kl
∴ M - m = \(\large{\frac{kl}{μg}}\)
∴ m = M - \(\large{\frac{kl}{μg}}\)