図1のように、滑車Aが天井に固定されている。水平な床面上に質量 M の小物体Bを置き、Bに伸び縮みしない糸をつけて滑車にかけ、糸の他端に砂を入れた容器Cをつるした。はじめ、容器Cと砂の質量の和が m のとき、糸と床のなす角が θ で小物体Bと容器Cは静止していた。その後、容器Cに砂を加えてその質量を大きくしていくと、小物体Bは床を右向きにすべり始めた。小物体Bと床の間の静止摩擦係数を μ 、重力加速度の大きさを g とする。ただし、糸と滑車の質量は無視でき、滑車はなめらかにまわるものとする。
（問1）はじめ、小物体Bと容器Cが静止しているとき、Bが床から受ける摩擦力 F の大きさはいくらか。
（問2）容器Cに砂を加えて小物体Bが運動し始めたときの容器Cと砂の質量の和はいくらか。
#センター05本試
（問1）
摩擦力 F は水平方向の力です。水平方向左向きです。いま小物体が静止しているということは、その摩擦力と水平方向右向きの何らかの力がつり合っているということです。
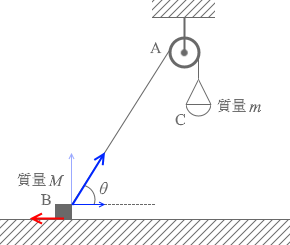何らかの水平方向右向きの力というのは、張力の水平成分のことです。
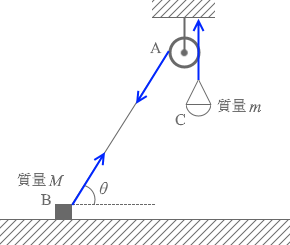張力というのはどこもかしこも同じ大きさです。
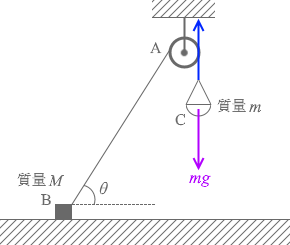そして、この張力を生み出しているのは砂に掛かる重力 mg です。
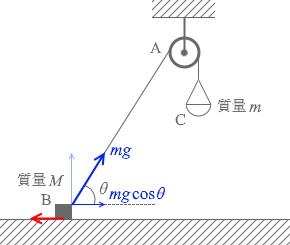つまり、何らかの水平方向右向きの力というのは mgcosθ です。
この力と摩擦力がつり合っていることによって小物体は静止しているので、摩擦力の大きさもこの力と同じで、mgcosθ です。
（余談）
摩擦力 mgcosθ の中に μ が含まれてないのは納得されますでしょうか。いま問われているのは静止摩擦力であり、これには μ は関わりがありません。関わるのは”最大”静止摩擦力です。動き出す瞬間の摩擦力です。下の（問2）の摩擦力です。
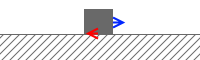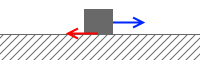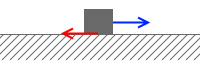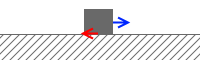物体が静止している間の摩擦力は静止摩擦力であり、これは外力に対抗する分の力だけを発揮するものです。
このことを分かっているかどうかというのがこの問題の主旨です。
あと、鉛直方向の力について考えてみますと、
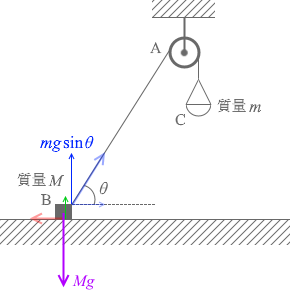小物体Bには重力 Mg が掛かかっていて、糸が無ければこれを逆向きにしたものが垂直抗力になるのですが、張力の鉛直成分 mgsinθ によって上向きに引っ張られることによって、小物体を床に押し付ける力が弱まっています。垂直抗力は押し付ける力を逆向きにしたものですから、垂直抗力も弱まります。垂直抗力を N としますとその大きさは
N = Mg - mgsinθ
です。
（問2）容器Cに砂を加えて小物体Bが運動し始めたときの容器Cと砂の質量の和はいくらか。
求める質量を m' と置きますと、
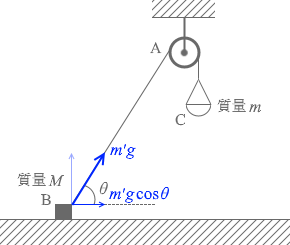張力は、問1で求めたのと同様に
m'g
で、小物体Bを水平方向に引っ張る力は
m'gcosθ
です。この力は砂を加えていくと大きくなっていきます。
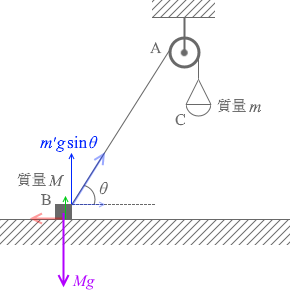また、このときの垂直抗力を N' と置きますと、上の（余談）で解説したのと同様にその大きさは
N' = Mg - m'gsinθ
です。この力は砂を加えていくと小さくなっていきます。
この問題における摩擦力は静止摩擦力ではなくて”最大”静止摩擦力であり、それは垂直抗力に静止摩擦係数を掛けたものです。つまり、
μN' = μ(Mg - m'gsinθ)
であり、小物体Bが運動し始める瞬間というのは、この最大静止摩擦力と小物体Bを水平方向に引っ張る力が等しくなった瞬間です。すなわち、
m'gcosθ = μ(Mg - m'gsinθ)
であり、
∴ m'cosθ = μ(M - m'sinθ)
∴ μm'sinθ + m'cosθ = μM
∴ m' = \(\large{\frac{μM}{μ\sinθ+\cosθ}}\)
と求まります。