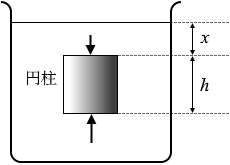
図4のように、底面積 S 、高さ h の円柱が密度 ρ の液体中にある。液面と円柱の上面の距離を x とする。液体中の圧力は、深さに比例する圧力と大気圧 p の和になることを考慮すると、円柱の上面にはたらく力の大きさはいくらか。また、下面にはたらく力の大きさはいくらか。ただし、重力加速度の大きさを g とする。
#センター06本試
図4のように、底面積 S 、高さ h の円柱が密度 ρ の液体中にある。液面と円柱の上面の距離を x とする。液体中の圧力は、深さに比例する圧力と大気圧 p の和になることを考慮すると、円柱の上面にはたらく力の大きさはいくらか。また、下面にはたらく力の大きさはいくらか。ただし、重力加速度の大きさを g とする。

#センター06本試
(以下 p と ρ を見間違いないようご注意ください。)
流体の圧力の関係式 p = p0 + ρgh に本問の量を当てはめますと、
上面での圧力: p上 = p + ρgx
下面での圧力: p下 = p + ρg(x + h)
(圧力)というのは(力)を(面積)で割ったものであるから、(力)は(圧力)と(面積)を掛けたものであり、
上面にはたらく力: \(\{\) p + ρgx \(\}\) × S = ρSxg + pS
下面にはたらく力: \(\{\) p + ρg(x + h) \(\}\) × S = ρS(h + x)g + pS
(余談)
上の2式の差を求めますと、
\(\{\) ρS(h + x)g + pS \(\}\) - \(\{\) ρSxg + pS \(\}\)
= \(\{\) ρS(h + x)g \(\}\) - \(\{\) ρSxg \(\}\)
= ρShg 円柱の体積を V と置きますと
= ρVg
となり、これが浮力の式です。
なお本問では、円柱が上昇するのか下降するのかはわかりません。浮き沈みは、液体の密度と円柱の密度と、どちらが大きいかに依ります。