密度 ρ 、体積 V の液体を入れた容器が、台ばかりにのっている。図2のように、密度 ρ' 、体積 V' の球(ρ' > ρ)を細いひもで上からつって、液体中で静止させた。このとき、はかりが示す力について考えよう。ただし、容器の質量は無視できるものとし、重力加速度の大きさを g とする。
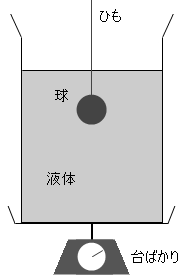
(問4)はかりが示す力の大きさはいくらか。
(問5)次にひもを切り離すと球は下降していき、容器の底に達して静止した。静止後にはかりが示す力の大きさはいくらか。
#センター08追試
密度 ρ 、体積 V の液体を入れた容器が、台ばかりにのっている。図2のように、密度 ρ' 、体積 V' の球(ρ' > ρ)を細いひもで上からつって、液体中で静止させた。このとき、はかりが示す力について考えよう。ただし、容器の質量は無視できるものとし、重力加速度の大きさを g とする。

(問4)はかりが示す力の大きさはいくらか。
(問5)次にひもを切り離すと球は下降していき、容器の底に達して静止した。静止後にはかりが示す力の大きさはいくらか。
#センター08追試
(問4)
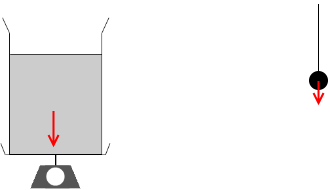 もし、液体と球が別々に存在するとしますと、液体には ρVg の重力が掛かり、球には ρ'V'g の重力が掛かり、
もし、液体と球が別々に存在するとしますと、液体には ρVg の重力が掛かり、球には ρ'V'g の重力が掛かり、
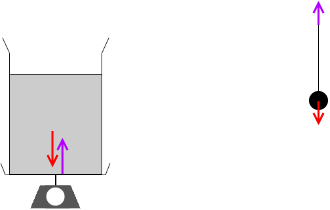 台ばかりは ρVg の力で支え、ひもは ρ'V'g の張力で上に引っ張っていることになります。
台ばかりは ρVg の力で支え、ひもは ρ'V'g の張力で上に引っ張っていることになります。
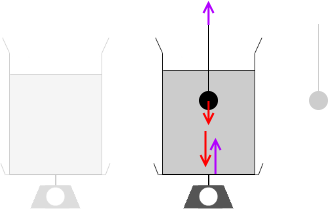 液体と球が一緒になった場合でも、液体と球の合計の重さは変わらず ρVg + ρ'V'g であり、こららを支える力の合計も(上向きで)ρVg + ρ'V'g です。
液体と球が一緒になった場合でも、液体と球の合計の重さは変わらず ρVg + ρ'V'g であり、こららを支える力の合計も(上向きで)ρVg + ρ'V'g です。
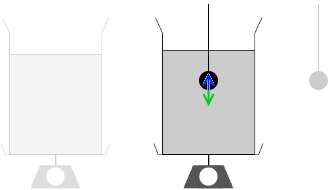 しかし、このとき浮力↑がはたらきますので、ひもの負担はその分、軽減されます。浮力がはたらくということは反作用の力↓が下向きにはたらくということでもあり、台ばかりの負担はその分、増加します。
しかし、このとき浮力↑がはたらきますので、ひもの負担はその分、軽減されます。浮力がはたらくということは反作用の力↓が下向きにはたらくということでもあり、台ばかりの負担はその分、増加します。
球にはたらく浮力の大きさは
ρV'g
です。(ρVg でも ρ'V'g でもなく ρV'g です。本編の解説をよくお読みください。)
ひもの負担は ρ'V'g から ρ'V'g - ρV'g へと軽減され、
台ばかりの負担は ρVg から ρVg + ρV'g へと増加します。
ひもと台ばかりを合わせたトータルの負担は変化しません。
答えは ρVg + ρV'g = ρ(V + V')g です。
(余談)
この問題は、
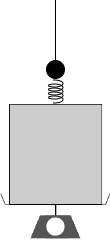 左図のように、物体の上にバネを載せて(バネの質量は無いものとする)、そのまた上に物体を載せて、ひもでつり下げたのと同じようなものです。バネによって、ひもの負担が軽減され、台ばかりの負担が増加します。軽減された分と増加した分は大きさが同じです。
左図のように、物体の上にバネを載せて(バネの質量は無いものとする)、そのまた上に物体を載せて、ひもでつり下げたのと同じようなものです。バネによって、ひもの負担が軽減され、台ばかりの負担が増加します。軽減された分と増加した分は大きさが同じです。
違いは、この場合はひもの張力をさじ加減で決めることができることです。バネが自然長の長さになるくらい強く引っ張ることもできますし、全く引っ張らずにひもをたるませることもできます。上の問題では、浮力の大きさは決まっていて、球を静止させるためには張力の大きさも決まってしまいます。
(問5)
球が底に達して静止しても浮力ははたらき続けます。同時にその反作用もはたらき続けます。しかしこの2つの力は相殺され、無いのと同然になります。ひもが切り離されれば液体と球の合計の重さ ρVg + ρ'V'g は全て台ばかりに掛かります。トータルの負担は常に ρVg + ρ'V'g です。ひもが無くなれば台ばかりだけでこれを負担することになります
上のバネの例を想像すると分かりやすいかもしれません。
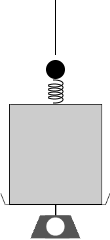 ひもが切れれば
ひもが切れれば
2つの物体の重さは台ばかりのみに掛かります。
。ひもがあれば浮力は意味をなしますが、ひもが無ければ、台ばかりにとって浮力は無意味です。このような場合の浮力や反作用の力を「内力」といいます。ひもがつながっているときは内力とはいいません。外界に影響を与えるからです。
答えは ρVg + ρ'V'g = (ρV + ρ'V')g です。