図2のように、長方形ABCDを上板とする水平で滑らかな机がある。点Aから点Eに向かって、また点Bから点Fに向かって、同じ質量の小物体を同じ速さで同時に発射したところ、二つの物体は点EとFで机を離れ、空中で衝突した。AB = 3a、DE = CF = a とし、小物体が発射されてから点E、Fで机を離れるまでの時間を T とする。二つの小物体が机を離れてから空中で衝突するまでの時間はいくらか。
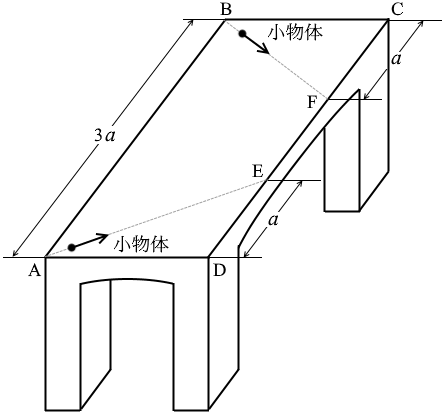
#センター04追試
図2のように、長方形ABCDを上板とする水平で滑らかな机がある。点Aから点Eに向かって、また点Bから点Fに向かって、同じ質量の小物体を同じ速さで同時に発射したところ、二つの物体は点EとFで机を離れ、空中で衝突した。AB = 3a、DE = CF = a とし、小物体が発射されてから点E、Fで机を離れるまでの時間を T とする。二つの小物体が机を離れてから空中で衝突するまでの時間はいくらか。
#センター04追試
一見複雑に見える問題ですが、これは『水平投射』や『モンキーハンティング』で説明したように、しっかり x成分、y成分（この場合 z成分も）に分解して考えることができるか、を問うてる問題です。
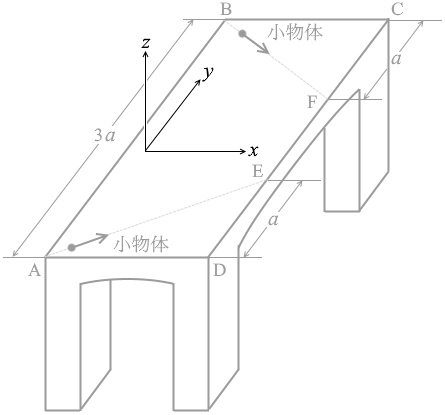たとえば左図のように xyz座標を当てはめたときに、二つの小物体は z成分と x成分がまったく同じ動きをします。
z成分は、途中まで静止していて途中から自由落下をします。
x成分は、ずっと等速運動です。
二つの物体は y成分だけ異なる動きをします。ですので、y成分さえ一致すれば、x成分も y成分も z成分も一致することになり、これはつまり、衝突する、ということになります。
二つの物体の y成分の動きを考えますと、
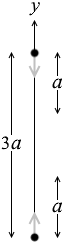二つの小物体の y成分が一致するのは真ん中の地点で、そこまでずっと等速で進んでいくわけですが、a 進むのに T だけ時間が掛かっているので、残りの \(\large{\frac{a}{2}}\) 進むのには \(\large{\frac{T}{2}}\) だけ時間が掛かるはずです。
というわけで、二つの小物体が机を離れて空中で衝突するまでの時間は \(\large{\frac{T}{2}}\) です。