最高点、水平到達距離
斜方投射における最高点に達するまでの時間、高さ、水平到達距離などを求めてみます。
斜方投射（鉛直上向きが正。θ は水平とのなす角、仰角。）
速度 vx = v0 cosθ vy = v0 sinθ - g t
位置 x = v0 cosθ・t y = v0 sinθ・t - \(\large{\frac{1}{2}}\) g t2
軌道の式 y = tanθ・x - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x2
最高点に達するまでの時間
最高点に達するとき、鉛直方向の速度 vy は 0 になるから＊上昇していきながら徐々にスピードが遅くなり、スピードが 0 になったときに、もうそれ以上、上にいけなくなるのだから、そのときが最高点。
閉じる、最高点に達するまでの時間 tH を求めると、
vy = v0sinθ - g tH = 0
∴ g tH = v0sinθ
∴ tH = \(\large{\frac{v_0\sin\theta}{g}}\)
最高点の高さ
tH = \(\large{\frac{v_0\sin\theta}{g}}\) を y = v0 sinθ・t - \(\large{\frac{1}{2}}\) g t2 に代入して、最高点の高さ yH を求めてみます。
yH = v0sinθ・\(\large{\frac{v_0\sin\theta}{g}}\) - \(\large{\frac{1}{2}}\) g \(\bigl(\large{\frac{v_0\sin\theta}{g}}\bigr)^2\)
= \(\large{\frac{{v_0}^2\sin^2\theta}{g}}\) - \(\large{\frac{{v_0}^2\sin^2\theta}{2\ g}}\)
= \(\large{\frac{2{v_0}^2\sin^2\theta}{2\ g}}\) - \(\large{\frac{{v_0}^2\sin^2\theta}{2\ g}}\)
= \(\large{\frac{{v_0}^2\sin^2\theta}{2\ g}}\)
最高点に達したときの水平距離
tH = \(\large{\frac{v_0\sin\theta}{g}}\) を x = v0 cosθ・t に代入して最高点に達したときの水平距離 xH を求めてみます。
xH = v0 cosθ・\(\large{\frac{v_0\sin\theta}{g}}\)
= \(\large{\frac{{v_0}^2\sin\theta\cos\theta}{g}}\)
放物線の頂点
xH と yH を求める作業は、数学における放物線の頂点を求める作業と同じです。数学において、
y = a x2 + b x + c の放物線のグラフの頂点は ( -\(\large{\frac{b}{2a}}\) , -\(\large{\frac{b^2-4ac}{4a}}\) ) である
という公式があると思いますが、斜方投射の軌道の式
y = tanθ・x - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x2
= - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x2 + tanθ・x + 0
に当てはめて解くと、 ( xH , yH ) が求まります。
水平到達距離
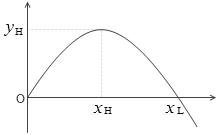xH を2倍すると、それは水平到達距離（水平飛距離） xL になります。＊同様に、tH を2倍すると、地面から物体を投げ上げて再び地面に戻ってくるまでの時間になります。
閉じる
xL = 2 xH
= \(\large{\frac{2\ {v_0}^2\sin\theta\cos\theta}{g}}\)
= \(\large{\frac{{v_0}^2\sin2\theta}{g}}\) (三角関数の2倍角の公式 2 sinθ cosθ = sin2θ より)
これは、数学における放物線と x軸との交点を求める作業と同じです＊x軸と交わるということは y の値が 0 ということだから、
斜方投射の軌道の式において y = 0 。つまり、
y = tanθ・x - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x2 = 0
∴ - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x2 + tanθ・x = 0
∴ - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x \(\biggl(\) x - \(\large{\frac{{2\ v_0}^2\cos^2\theta}{g}}\) tanθ \(\biggr)\) = 0
∴ - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x \(\biggl(\) x - \(\large{\frac{{2\ v_0}^2\cos^2\theta}{g}}\) \(\large{\frac{\sin\theta}{\cos\theta}}\) \(\biggr)\) = 0
∴ - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x \(\biggl(\) x - \(\large{\frac{{2\ v_0}^2\sin\theta\cos\theta}{g}}\) \(\biggr)\) = 0
∴ - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x \(\biggl(\) x - \(\large{\frac{{v_0}^2\sin2\theta}{g}}\) \(\biggr)\) = 0
∴ x = 0 , \(\large{\frac{{v_0}^2\sin2\theta}{g}}\)
この2つの値のうちの x = 0 というのはスタート地点のことだから、求める xL は、
xL = \(\large{\frac{{v_0}^2\sin2\theta}{g}}\)
閉じる。
水平到達距離が最大になる角度
初速度 v0 が一定のとき、角度をどのようにしたら一番遠くまで飛ぶかを考えてみますと、それは
xL = \(\large{\frac{{v_0}^2\sin2\theta}{g}}\)
のうちの sin2θ が最大となるときです。sin2θ は - 1 から 1 までの値をとります。つまり最大値は 1 です。 sin2θ = 1 、つまり 2θ = 90° のとき sin2θ が 1 となり最大となります。これはつまり、θ = 45° のとき xL が最大となるということです。＊ちなみに、
2θ = 80° のときも 2θ = 100° のときも sin2θ の値は同じ。つまり θ = 40° のときも θ = 50° のときも水平到達距離は同じです。
同様に、
44° のときと 46° のときも同じ、
30° のときと 60° のときも同じ、
15° のときと 75° のときも同じです。
閉じる
空気抵抗がある場合については補足ページをご覧ください。
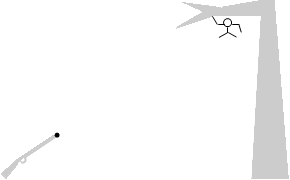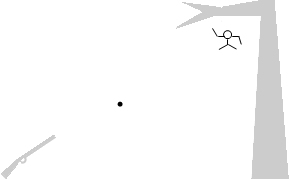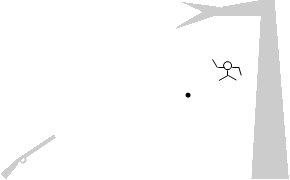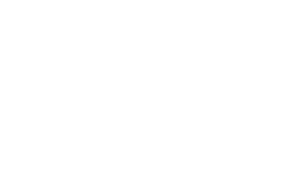木の枝にぶら下がっている猿に狙いを定めて銃を撃つと、その音に驚いて手を離して落下した猿に必ず当たります。銃の弾は一直線に飛ぶわけではなく、重力によって少し下降します。それなのに必ず猿に命中するのです。このことをモンキーハンティングといいます。
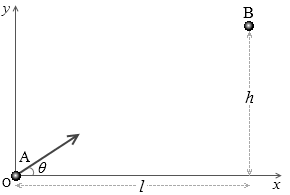左図のように、原点Oに物体A、( l , h ) の位置に物体Bがあるとします。今、物体Aを物体Bに向けて、つまり水平とのなす角を θ とするとき