地上で、ある物体を鉛直方向に投げ上げた。このとき、物体の高さ y と時刻 t の関係は、図1に示すグラフのようになった。ただし、図1のグラフの横軸の1目盛りは1秒である。縦軸の1目盛りの大きさは記入していない。
（問1）最高点の高さはいくらか。ただし、重力加速度の大きさを 9.8 m/s2 とする。
（問2）火星上の重力加速度の大きさはおよそ 3.7 m/s2 である。火星上で、同じ物体を、同じ初速度で鉛直方向に投げ上げたとき、その運動を表すグラフはどのようになるか。最も適当なものを、次の①～④のうちから一つ選べ。ただし、グラフの目盛りは図1と同じものとする。
（問3）qG7FC
#センター06本試
（問1）最高点の高さはいくらか。ただし、重力加速度の大きさを 9.8 m/s2 とする。
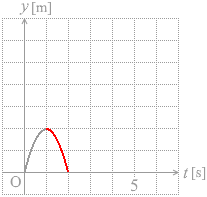
最高点から地表に落ちるまでの間は自由落下運動であり、その時間は、グラフから読み取ると 1.0秒間です。求める最高点の高さを y1 と置いて自由落下運動の変位の式（ y = \(\large{\frac{1}{2}}\)gt2 ）を立てますと、
y1 = \(\large{\frac{1}{2}}\)×9.8×1.02
∴ = 4.9 [m]
と求まります。
（別解：まず初速度を求める）
投げ上げてから 1.0秒後に速度が 0 になるので、初速度を v0 と置いて鉛直上方投射の速度の式（ v = v0 - gt ）を立てますと、
0 = v0 - 9.8×1.0
∴ v0 = 9.8 [m/s]
あるいは、
グラフより 2.0秒後に y = 0 となるので、鉛直上方投射の変位の式（ y = v0t - \(\large{\frac{1}{2}}\)gt2 ）を立てて、
0 = v0×2.0 - \(\large{\frac{1}{2}}\)×9.8×2.02
∴ v0×2.0 = \(\large{\frac{1}{2}}\)×9.8×2.02
∴ v0 = \(\large{\frac{1}{2}}\)×9.8×2.0
∴ v0 = 9.8 [m/s]
と求めることもできます。
この値を用いて鉛直上方投射の変位の式（ y = v0t - \(\large{\frac{1}{2}}\)gt2 ）を立てますと、
y1 = 9.8×1.0 - \(\large{\frac{1}{2}}\)×9.8×1.02
∴ = 9.8 - 4.9
∴ = 4.9 [m]
と求まります。
（問2）火星上の重力加速度の大きさはおよそ 3.7 m/s2 である。火星上で、同じ物体を、同じ初速度で鉛直方向に投げ上げたとき、その運動を表すグラフはどのようになるか。最も適当なものを、次の①～④のうちから一つ選べ。ただし、グラフの目盛りは図1と同じものとする。
最高点に達するまでの時間を t2 と置きます。初速度が（上で求めましたが）9.8 m/s で、最高点では速度が 0 であるわけですから、鉛直上方投射の速度の式（ v = v0 - gt ）を立てますと、
0 = 9.8 - 3.7×t2
∴ 3.7×t2 = 9.8
∴ t2 = \(\large{\frac{9.8}{3.7}}\) ≒ 2.6486 [s]
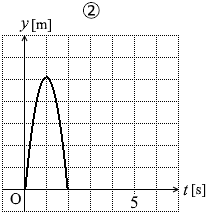
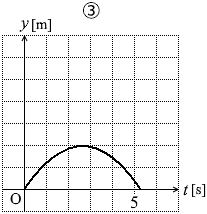
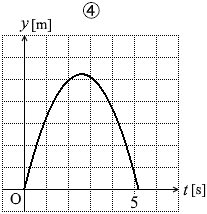
曲線の最高点で時刻がこのくらいになっているグラフは③か④です。
また、最高点の高さを y2 と置いて、鉛直上方投射の t を含まない式（ v2 - v02 = - 2gy ）を立てますと、
02 - 9.82 = - 2×3.7×y2
∴ 7.4×y2 = 9.82
∴ y2 = \(\large{\frac{9.8^2}{7.4}}\)
∴ ≒ 12.978 [m]
問1の結果より、図1の曲線の最高点の高さが 4.9 [m] であり、それと比べて最高点の高さが2倍強になっているグラフは ④ です。
（別解：放物線の頂点の座標を求めるという数学の知識を使って解く）
鉛直上方投射の変位の式（ y = v0t - \(\large{\frac{1}{2}}\)gt2 ）を立てますと、
y = 9.8×t - \(\large{\frac{1}{2}}\)×3.7×t2 平方完成の形に持って行きます
= 9.8t - \(\large{\frac{3.7}{2}}\)t2
= - \(\large{\frac{3.7}{2}}\)t2 + 9.8t
= - \(\large{\frac{3.7}{2}}\)(t2 - \(\large{\frac{2×9.8}{3.7}}\)t)
= - \(\large{\frac{3.7}{2}}\)\(\Big\{\)(t - \(\large{\frac{9.8}{3.7}}\))2 - (\(\large{\frac{9.8}{3.7}}\))2\(\Big\}\)
= - \(\large{\frac{3.7}{2}}\)(t - \(\large{\frac{9.8}{3.7}}\))2 + \(\large{\frac{3.7}{2}}\)(\(\large{\frac{9.8}{3.7}}\))2
= - \(\large{\frac{3.7}{2}}\)(t - \(\large{\frac{9.8}{3.7}}\))2 + \(\large{\frac{9.8^2}{2×3.7}}\)
= - \(\large{\frac{3.7}{2}}\)(t - \(\large{\frac{9.8}{3.7}}\))2 + \(\large{\frac{9.8^2}{7.4}}\)
以上により、最高点の座標 ( t2 , y2 ) は ( \(\large{\frac{9.8}{3.7}}\) , \(\large{\frac{9.8^2}{7.4}}\) ) であり、上の結果と一致します。
（あるいは、難しい計算をしなくても、月面を歩く宇宙飛行士の映像から、なんとなく④が妥当ではないかと類推できます。）