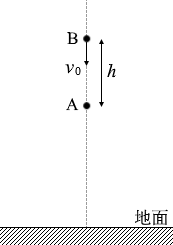
図1のように、ある高さの点から小球Aを静かに落とすと同時に、その点より h だけ鉛直上方の点から小球Bを速さ v0 で投げ下ろして、Aが地面に達する前にAとBを衝突させた。二つの小球が落下し始めてから衝突するまでの時間はいくらか。ただし、重力加速度の大きさを g とする。
#センター09追試
図1のように、ある高さの点から小球Aを静かに落とすと同時に、その点より h だけ鉛直上方の点から小球Bを速さ v0 で投げ下ろして、Aが地面に達する前にAとBを衝突させた。二つの小球が落下し始めてから衝突するまでの時間はいくらか。ただし、重力加速度の大きさを g とする。

#センター09追試
落下し始めてからの時間を t とし、初めに小球Bがあった地点を変位の基準点とし、下向きを正としますと、
小球Aの変位は、(自由落下運動の変位の式は y = \(\frac{1}{2}\)gt2)
h + \(\frac{1}{2}\)gt2
小球Bの変位は、(鉛直下方投射の変位の式は y = v0t + \(\large{\frac{1}{2}}\)gt2)
v0t + \(\large{\frac{1}{2}}\)gt2
衝突するということは変位が同じになるということだから上2式が等しくなり、
h + \(\frac{1}{2}\)gt2 = v0t + \(\large{\frac{1}{2}}\)gt2
∴ t = \(\large{\frac{h}{v_0}}\)
(別解)
同時に落下し始めた物体の相対位置は重力の影響を無視できることを知っていれば、いきなり、
h = v0t
と立式でき、暗算で解けます。