qGARB

（問1）
1
『慣性質量と重力質量』で少し説明しましたが、物体の質量が大きくなっても落下速度は変わりません。重力に引きつけられる力が大きくなりますが、動きにくさも大きくなるのでトータルで変わりません。

この惑星での重力加速度を g' としますと、自由落下運動の式は

　　　　　 速度　 v = g't

　　　　　 変位　 y = \(\frac{1}{2}\)g't²

　tを含まない式　v² = 2g'y

ですが、これらの中に m の量記号は出てきません。質量は無関係なのです。

答え ⑤ v は変わらず、T も変わらない

一応、高さ h から落下させるものとして、着地するときの速さ v 、着地するまでの時間 T を求めてみます。

三番目の式より、
　　　　v² = 2g'h

　∴　　v = \(\sqrt{2g'h}\)

二番目の式より、
　　　　h = \(\frac{1}{2}\)g'T²

　∴　　T = \(\sqrt{\frac{2h}{g'}}\)

2
初速度が大きくなれば、着地するときの速さ v も、着地するまでの時間 T も大きくなるのは直感的にわかると思います。

鉛直上方投射の式は

　　　　　 速度　 v = v₀ - g't

　　　　　 変位　 y = v₀t - \(\large{\frac{1}{2}}\)g't²

　tを含まない式　v² - v₀² = - 2g'y

ですが、各式に v₀ が含まれてますので、各量は初速度と何らかの関係があるはずです。

（高さ h から投げ上げて地面に着地する場合を考えると式が複雑になるので）、高さ 0 から投げ上げた場合を考えてみます。

三番目の式より、
　　　　v² - v₀² = - 2g' × 0

　∴　　v = v₀

二番目の式より、
　　　　0 = v₀T - \(\large{\frac{1}{2}}\)g'T²

　∴　　\(\large{\frac{1}{2}}\)g'T² = v₀T

　∴　　\(\large{\frac{1}{2}}\)g'T = v₀

　∴　　T = \(\large{\frac{2v_0}{g'}}\)

v も T も v₀ に比例します。

答え ① v は大きくなり、T は長くなる

（問2）
高さ h から初速度 0 で落下させたときの、高さ h と時間 T の関係は、上の問1で説明したように、

　　　　T = \(\sqrt{\frac{2h}{g'}}\)

であり、この式をグラフにしたものが図1です。ルートのグラフがわかりにくければ、上式の計算前の式

　　　　h = \(\frac{1}{2}\)g'T²

を考えてもらえば、

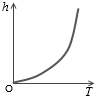このようになるとわかると思います。

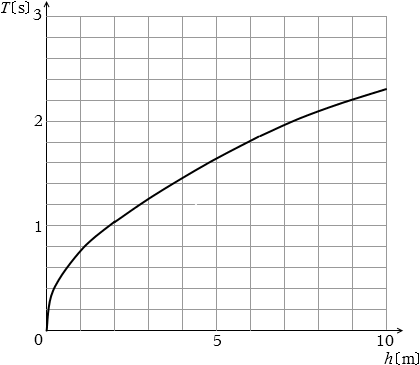
このグラフの h軸と T軸を入れ替えたものが図1です。

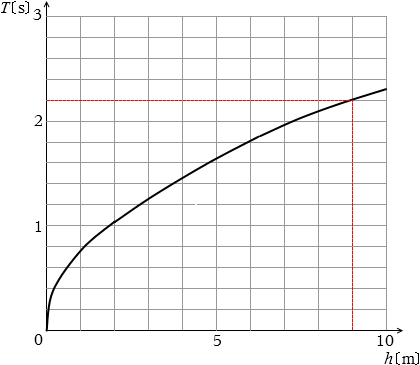そして、図1をよく見ますと、

h が 9.0m のときに、T が 2.2s であることが読み取れます。

これらの値を　T = \(\sqrt{\frac{2h}{g'}}\)　式に代入しますと、

（別に、h=6.0、T=1.8 を代入しても構いませんし、h = \(\frac{1}{2}\)g'T² 式に代入しても構いません。）

　　　　2.2 = \(\sqrt{\frac{2×9.0}{g'}}\)　

　∴　　2.2² = \(\large{\frac{2×9.0}{g'}}\)

　∴　　g' = \(\large{\frac{2×9.0}{2.2×2.2}}\) = \(\large{\frac{9.0}{2.2×1.1}}\) = \(\large{\frac{9.0}{2.42}}\) ≒ 3.7

答え ② 3.7

（余談）
3.7m/s² という値はだいたい火星の重力加速度くらいです。月の重力加速度はこれの半分くらいです。地球の重力加速度はもちろん 9.8m/s² です。