図2のように、水平から 60° の斜め上方に小球を発射する装置がある。小球を点Pから速さ \(v\) で鉛直な壁面に向かって打ち出した。小球は、高さが最高点に達したとき、点Qで壁面に垂直に衝突した。壁は点Pから水平方向にだけ \(l\) 離れており、点Qは点Pより \(h\) だけ高い位置にあった。ただし、小球は壁と垂直な鉛直面内を運動し、空気の抵抗は無視できるものとする。また、重力加速度の大きさを \(g\) とする。
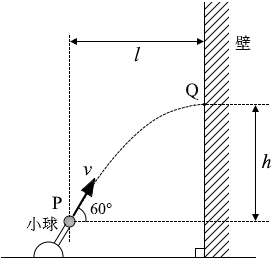
（問3）発射直後において、小球の水平方向の速さは \({\large\frac{v}{2}}\) である。発射から壁に衝突するまで、小球は水平方向には速度が一定の運動をする。発射直後から小球が壁に到達するまでの時間 \(t\) を式で表せ。
（問4）発射直後において、小球の鉛直方向の速さは \({\large\frac{\sqrt{3}}{2}v}\) である。小球は鉛直方向には加速度が一定の鉛直投げ上げ運動をし、点Qで鉛直投げ上げ運動の最高点に達する。\(h\) を式で表せ。
#センター20本試物理基礎
（基本事項として）
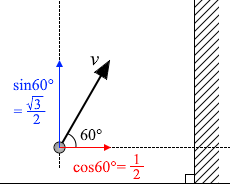この問題では親切に、発射直後の水平方向の速さが \({\large\frac{v}{2}}\)、鉛直方向の速さが \({\large\frac{\sqrt{3}}{2}v}\)、と示されていますが、これは 60° と角度が指定されているのでそこから導くことができるものです。他の問題ではふつう自分で導き出します。
（問3）
斜方投射においては水平方向には速度が一定の運動をするわけですから、時間は単純に距離を速さで割ったものであり、すなわち、
\(t = {\large\frac{l}{\frac{v}{2}}}\) = \({\large\frac{2l}{v}}\)
（問4）
鉛直投げ上げ運動の変位の式を立てますと、
\(h\) = \({\large\frac{\sqrt{3}}{2}v}t - {\large\frac{1}{2}}gt^2\) \(t\) の部分に上式を代入して
= \({\large\frac{\sqrt{3}}{2}}v・{\large\frac{2l}{v}} - {\large\frac{1}{2}}g({\large\frac{2l}{v}})^2\)
= \(\sqrt{3}l - 2g({\large\frac{l}{v}})^2\)
…なんですが、もし \(l\) を含まない式で答えろ、と指示された場合、鉛直投げ上げ運動の時間 \(t\) を含まない式を立てて求めます。
初速が \({\large\frac{\sqrt{3}}{2}v}\) で終速が 0 だから
\(0^2 - \big({\large\frac{\sqrt{3}}{2}v}\big)^2 = - 2gh\)
\(\big({\large\frac{\sqrt{3}}{2}v}\big)^2 = 2gh\)
\(3v^2 = 8gh\)
\(h\) = \({\large\frac{3v^2}{8g}}\)