斜方投射１

斜方投射 基礎物理範囲

斜め方向に初速を与えて、あとは重力の力にまかせて落下させるような運動を斜方投射といいます。

これも水平投射と同じく、2次元の運動であり、運動を水平方向と鉛直方向に分解して考えることができます。

斜方投射。

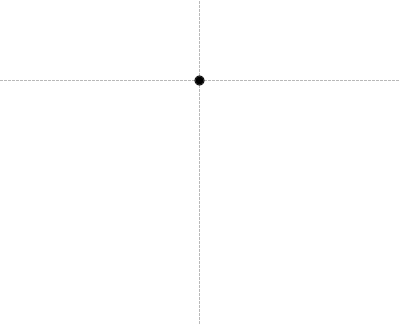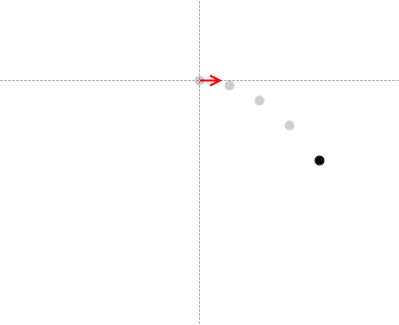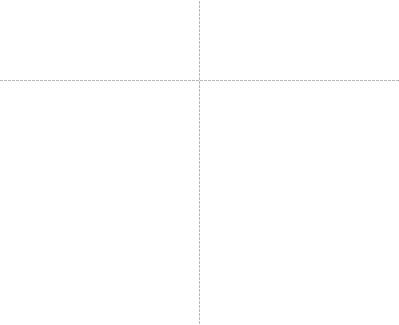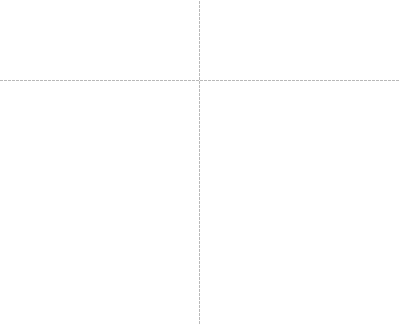
横軸の x軸に着目すると、速度が初速度のまま一定の等速直線運動（等速度運動）。

縦軸の y軸に着目すると、速度はだんだん遅くなり、やがて静止し、向きを変えて下向きに落ちていきます。これはまさに鉛直上方投射（等加速度直線運動）。

上図は斜め上に投げ出す運動を示しましたが、斜め下に投げ出す運動も斜方投射といいます。この場合、縦軸は鉛直下方投射になり、鉛直下向きが正となります（もしくは鉛直上向きが正のままとすることもあります）。

斜方投射を表す式 物理範囲

初速度を v₀ 、x軸方向の初速度を v_0 x 、y軸方向の初速度を v_0 y とし、水平とのなす角（仰角＊ぎょうかく。

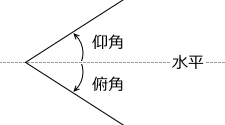
　閉じる）を θ とします。

x軸方向には、速度が初速度のまま一定の等速直線運動をし、この x軸方向の初速度は斜方投射の初速度の水平成分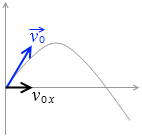＊ v_0 x = v₀ cosθ
　閉じるであるから、

　　　　速度　v_x = v_0 x = v₀ cosθ　　（一定）

　　　　位置　x = v_0 x t = v₀ cosθ・t

y軸方向には、鉛直投射運動 ＊鉛直投射には鉛直下方投射と鉛直上方投射がありますが、鉛直下方投射は鉛直上方投射に統合できます。つまり、鉛直上向きを正とし、初速度は負の値もとることとします。
そうすれば、
斜め上への斜方投射 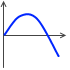にも、斜め下への斜方投射 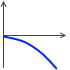にも、どちらにも対応できます。
　閉じるをし、この y軸方向の初速度は斜方投射の初速度の鉛直成分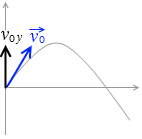＊ v_0 y = v₀ sinθ閉じるであり、鉛直上向きを正として、

　　　　速度　v_y = v_0 y - g t = v₀ sinθ - g t

　　　　位置　y = v_0 y t - \(\large{\frac{1}{2}}\) g t² = v₀sinθ・t - \(\large{\frac{1}{2}}\) g t²

さらに、x = v₀ cosθ・t　を　y = v₀sinθ・t - \(\large{\frac{1}{2}}\) g t²　に代入して t を消去すると、

　　　　y = v₀sinθ \(\bigl(\large{\frac{x}{v_0\cos\theta}}\bigr)\) - \(\large{\frac{1}{2}}\) g \(\bigl(\large{\frac{x}{v_0\cos\theta}}\bigr)^2\)

　　　　　= \(\bigl(\large{\frac{\sin\theta}{\cos\theta}}\bigr)\) x - \(\large{\frac{1}{2}}\) g \(\bigl(\large{\frac{x^2}{{v_0}^2\cos^2\theta}}\bigr)\)

　　　　　= tanθ・x - \(\large{\frac{g}{{2\ v_0}^2\cos^2\theta}}\) x²

これは斜方投射した物体の軌道を表す式であり、 y = (定数A)・x² + (定数B)・x　の形になっていますので x の2次関数であり、グラフの曲線は放物線になります。いま、鉛直上向きを正としていて (定数A) が負なので上に凸の放物線になります＊水平投射に関しても斜方投射に関しても、放物線は上に凸の形になるということです。当たり前ですが。
さらに、y = (定数A)・x² + (定数B)・x + (定数C)　における (定数C) の部分が 0 なのでこの放物線は原点を通ります。詳しくは数学の教科書を見てください。
(定数B) も 0 だとするとそれは水平投射の軌道を表す式ということになります。
　 閉じる。

この軌道の式を覚えるのは大変かもしれません。導出方法をしっかり覚えてください。