qO7V8　■わかりやすい高校物理の部屋■

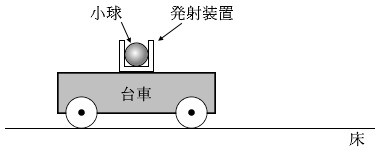
図1のように、小球を速さ \(v_0\) で鉛直上向きに発射できる装置を備えた台車が水平な床の上にある。ただし、重力加速度の大きさを \(g\) とし、空気抵抗は無視できるものとする。

（問1）時刻 \(t\)=0 に、静止した台車から小球を打ち出した。小球が最高点に到達する時刻を表す式として正しいものを、次の①～⑥のうちから一つ選べ。

　①　\(\large\frac{v_0}{2g}\)　　②　\(\large\frac{v_0}{g}\)　　③　\(\large\frac{2v_0}{g}\)

　④　\(\large\frac{{v_0}^2}{2g}\)　　⑤　\(\large\frac{{v_0}^2}{g}\)　　⑥　\(\large\frac{2{v_0}^2}{g}\)

（問2）次の文章中の空欄ア・イに入れる語句の組合せとして最も適当なものを、下の①～⑨のうちから一つ選べ。

次に、一定の速度で動く台車から小球を打ち出す。このとき小球が到達する最高点の高さは、静止した台車から打ち出した場合と比べてア、小球は発射装置のイに落下する。

#センター18本試物理基礎

　　\(v = v_0 + at\)

　　\(x = {v_0}t + {\large\frac{1}{2}}at^2\)

　　\(v^2 - {v_0}^2 = 2ax\)

であり、鉛直上方投射の公式は

　　\(v = v_0 - gt\)　　……❶

　　\(y = {v_0}t - {\large\frac{1}{2}}gt^2\)　　……❷

　　\(v^2 - {v_0}^2 = -2gy\)　　……❸

でありますが、❶式を使って解いてみますと、

小球が最高点に到達した瞬間は速度は 0 になっているから

　　\(0 = v_0 - gt\)

∴　\(t = \textcolor{yellow}{\underline{\textcolor{black}{\large\frac{v_0}{g}}}}\)

答えは ② です。

（無理矢理❸式を使って解くと）

　　\(0^2 - {v_0}^2 = -2gy\)

　　∴　\(y = \large\frac{{v_0}^2}{2g}\)

❷式に代入して

　　　\({\large\frac{{v_0}^2}{2g}} = {v_0}t - {\large\frac{1}{2}}gt^2\)　　移項して

∴　\({\large\frac{1}{2}}gt^2 - {v_0}t + {\large\frac{{v_0}^2}{2g}} = 0\)　　\({\large\frac{2}{g}}\)を掛けて

∴　\(t^2 - 2{\large\frac{v_0}{g}}t + {\large\frac{{v_0}^2}{g^2}} = 0\)　　平方完成して

∴　　\((t - {\large\frac{v_0}{g}})^2 = 0\)

∴　　　　\(t = \large\frac{v_0}{g}\)

（問2）
この小球の運動は斜方投射でありますが、斜方投射は鉛直成分と水平成分に分解して考えることができます。そしてこの鉛直成分と水平成分は互いに影響を及ぼし合いません。

鉛直成分の運動は問1となんら変わりません。つまり、静止した台車から打ち出した場合と比べて 変わりません 。

水平成分の運動は台車の運動と同一です。つまり、小球は発射装置の中に落下します。

答えは ⑨ です。