糸がピンと張っているときは、物体Aと物体Bは一つの物体とみなすことができますが、糸がたるみ始めた後は別々の物体と考えなければなりません。
(まず、ピンと張っているときの力学的エネルギーを考えます)
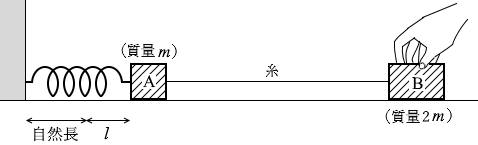 手で押さえて l だけ伸びているときの力学的エネルギーは、
手で押さえて l だけ伸びているときの力学的エネルギーは、
運動エネルギー : 0
弾性エネルギー : \(\large{\frac{1}{2}}\)kl2
だから、0 + \(\large{\frac{1}{2}}\)kl2 ……①
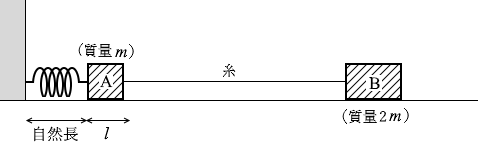 自然長のところまで来たときの力学的エネルギーは、そのときの物体A、物体Bの速さを v0 と置いて、
自然長のところまで来たときの力学的エネルギーは、そのときの物体A、物体Bの速さを v0 と置いて、
運動エネルギー : \(\large{\frac{1}{2}}\)(m+2m)v02
弾性エネルギー : 0
だから、\(\large{\frac{1}{2}}\)(m+2m)v02 + 0 ……②
力学的エネルギー保存の法則により ① = ② であるから、
\(\large{\frac{1}{2}}\)kl2 = \(\large{\frac{1}{2}}\)(m+2m)v02
∴ kl2 = 3mv02
∴ v02 = \(\large{\frac{kl^2}{3m}}\) ……③
(たるみ始めたら物体Aと物体Bは別個の物体)
自然長に達するまでは糸はピンと張っていて、物体Aは物体Bを引っ張っているので、2つは一体とみなすことができましたが、それ以降は糸がたるむので一体とはみなせません。ばねが今度は逆の右方向に押し始めるので物体Aのスピードが物体Bのスピードより遅くなります。
以降は、物体Aのみの力学的エネルギーを考えます。
 自然長の位置にいる物体Aの力学的エネルギーは、
自然長の位置にいる物体Aの力学的エネルギーは、
運動エネルギー : \(\large{\frac{1}{2}}\)mv02
弾性エネルギー : 0
だから、\(\large{\frac{1}{2}}\)mv02 + 0 ……④
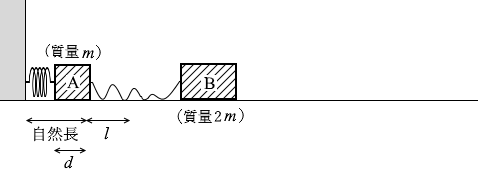 最も縮む幅を d と置くと、その位置での物体Aの力学的エネルギーは、
最も縮む幅を d と置くと、その位置での物体Aの力学的エネルギーは、
運動エネルギー : 0
弾性エネルギー : \(\large{\frac{1}{2}}\)kd2
だから、0 + \(\large{\frac{1}{2}}\)kd2 ……⑤
力学的エネルギー保存の法則により ④ = ⑤ であるから、
\(\large{\frac{1}{2}}\)mv02 = \(\large{\frac{1}{2}}\)kd2
v02 の大きさは③で調べてあるのでこれを代入して、
\(\large{\frac{1}{2}}\)m\(\large{\frac{kl^2}{3m}}\) = \(\large{\frac{1}{2}}\)kd2 ……⑥
∴ \(\large{\frac{l^2}{3}}\) = d2
∴ d = \(\large{\frac{1}{\sqrt{3}}}\)l
(余談:\(\large{\frac{1}{\sqrt{3}}}\) はどこから来ているのか)
といいますと、それは⑥式の
\(\large{\frac{1}{2}}\)m\(\large{\frac{kl^2}{\textcolor{#930}{3m}}}\) = \(\large{\frac{1}{2}}\)kd2
の m と 3m であり、さらにたどると、m は④式から来ていて、つまりは物体Aの質量であり、3m は③式(さらには②式)から来ていて、つまりは物体Aと物体Bの質量の合計のことです。
ということは、d というのは
d = \(\sqrt{\frac{A}{A+B}}\) l
というように表現できるということです。
A = m 、B = 3m であれば、
d = \(\sqrt{\frac{1}{4}}\) l
で、A = 2m 、B = m であれば、
d = \(\sqrt{\frac{2}{3}}\) l
で、A = m 、B = 9m であれば、
d = \(\sqrt{\frac{1}{10}}\) l
で、A = 9m 、B = m であれば、
d = \(\sqrt{\frac{9}{10}}\) l
です。
そして、d は l を超えることはありません。当然ですが。
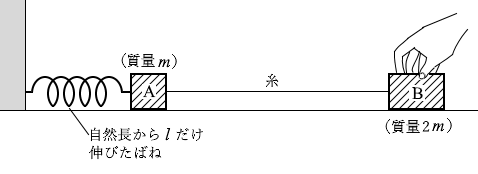
 手で押さえて l だけ伸びているときの
手で押さえて l だけ伸びているときの 自然長のところまで来たときの力学的エネルギーは、そのときの物体A、物体Bの速さを v0 と置いて、
自然長のところまで来たときの力学的エネルギーは、そのときの物体A、物体Bの速さを v0 と置いて、 最も縮む幅を d と置くと、その位置での物体Aの力学的エネルギーは、
最も縮む幅を d と置くと、その位置での物体Aの力学的エネルギーは、