手を離した直後は糸がピンと張っているので物体Aと物体Bは合わせて1つの物体とみなすことができます。
l だけ伸びたばね は kl
1つに合わせた物体の質量は m + 2m であり、これの加速度を a と置いて運動方程式 を立てますと、
(m + 2m )a = kl
となり、これを解きますと、
∴ a = \(\large{\frac{kl}{3m}}\) ……①
と導かれます。
(物体Aと物体Bを別個として考える場合は)
張力 を T
物体A : ma = kl T
物体B : 2ma = T
という運動方程式が立てられ、この連立方程式を解くと上と同じ結果が導かれます。
(このとき物体Aに掛かる張力と物体Bに掛かる張力が等しいのは力のつり合いではなく作用・反作用の法則 です。念のため)
(手を離した瞬間について考えますと)
T m \(\large{\frac{kl}{3m}}\) = \(\large{\frac{2}{3}}\)kl
と張力 T が求められ、ばねが物体Aを引く力 kl
(次に、手を離してから糸の張力の大きさが 0 になるまでの間のばねの伸びを l x T x kl x m + 2m )a = kl x
物体Aの運動方程式は ma = kl x T x
物体Bの運動方程式は 2ma = T x
①'式を③'式に代入して、
T x m \(\large{\frac{kl_x}{3m}}\) = \(\large{\frac{2}{3}}\)kl x
であり、kl x
つまり、手を離した瞬間も、手を離してから糸の張力の大きさが 0 になるまでの間も、まったく同じ結果になり、張力の大きさは、ばねが物体Aを引く力の大きさの \(\large{\frac{2}{3}}\) 倍 になっています。
(余談:質量の比)
T 2m \(\large{\frac{kl}{\textcolor{#930}{3m}}}\) = \(\large{\frac{2}{3}}\)kl
の 2m と 3m から来ていて、さらに、
2m は③式、③'式から来ていて、つまりは物体Bの質量のことで、
3m は①式、①'式から来ていて、つまりは物体Aと物体Bを合わせた質量のことです。
m 、物体Bの質量が 3m だったりした場合は張力 の大きさは引く力 の \(\large{\frac{3}{4}}\) 倍ですし、
m 、物体Bの質量が 7m だった場合は張力 の大きさは引く力 の \(\large{\frac{7}{8}}\) 倍で、
応用問題として、
*
同じ質量の物体を5連結したものを引っ張った場合の力の様子は、
5F で引っ張ったとすると、次の糸は 4F で引っ張り、それ以降は 3F 、2F 、F 閉じる
(あと、ばねを使って引いても手を使って引いても関係ありませんので、一応)
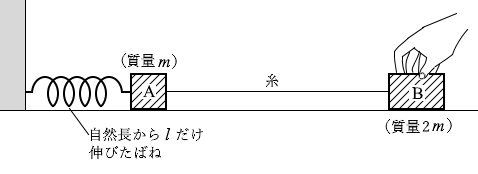
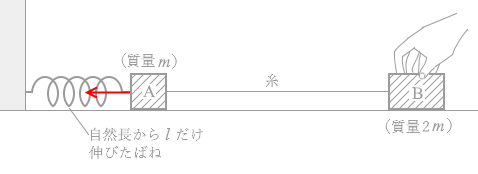 l だけ伸びた
l だけ伸びた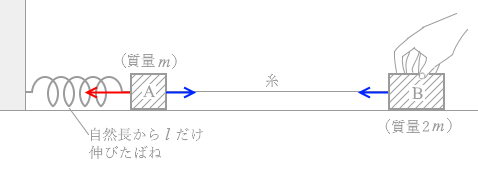
 もし物体Aの質量が m 、物体Bの質量が 3m だったりした場合は
もし物体Aの質量が m 、物体Bの質量が 3m だったりした場合は 物体Aの質量が m 、物体Bの質量が 7m だった場合は
物体Aの質量が m 、物体Bの質量が 7m だった場合は 逆側から引けば \(\large{\frac{1}{8}}\) 倍です。
逆側から引けば \(\large{\frac{1}{8}}\) 倍です。 多数連結されている物体を引っ張った場合の各張力はいくらであるかを問うなんて問題が考えられますが、本問題を理解していれば簡単だと思います。(加速中であり、静止してませんので、力のつり合いの問題ではありません)
多数連結されている物体を引っ張った場合の各張力はいくらであるかを問うなんて問題が考えられますが、本問題を理解していれば簡単だと思います。(加速中であり、静止してませんので、力のつり合いの問題ではありません) このようになります。
このようになります。