ばねの一端を固定し、他端におもりを付け、往復運動できるようにしたものをばね振り子といいます。ばねに質量が無く、空気抵抗や床面との摩擦も無いとすると、水平に置かれたばね振り子のおもりにはたらく力は弾性力だけです。鉛直に吊るした場合のばね振り子のおもりにはたらく力は弾性力と重力だけです。弾性力も重力も保存力であり、力学的エネルギー保存の法則が成り立ちます。
『単振り子の力学的エネルギー』と同じように力学的エネルギー保存の法則を使って、ばね振り子のおもりの速さを求めてみます。
本項では、ばね振り子のおもりの各瞬間の速さが力学的エネルギー保存の法則によって求められるという話をします。ばね振り子が単振動することに着目してその周期などを求める話は『ばね振り子』項でします。
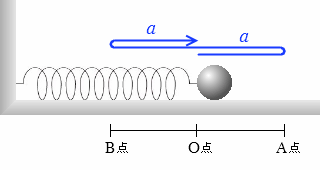なめらかな水平面上で、ばね定数 k [N/m] のばねの一端を固定し、他端に質量 m [kg] のおもりを付けたばね振り子を、自然長から a [m] だけ引っ張って離すと、おもりは自然長の位置O点を中心にして、振幅 a [m] の往復運動をします。
| 力学的エネルギー | 運動エネルギー | 弾性エネルギー | 原点からの変位 | 弾性力 | 速さ | |
|---|---|---|---|---|---|---|
| A点（最右端） | EA | KA = 0 | UA = \(\large{\frac{1}{2}}\)ka2 | a | - ka | vA = 0 |
| X点（任意の位置） | EX | KX = \(\large{\frac{1}{2}}\)mvx2 | UX = \(\large{\frac{1}{2}}\)kx2 | x | - kx | vx |
| O点（自然長） | EO | KO = \(\large{\frac{1}{2}}\)mvO2 | UO = 0 | 0 | 0 | vO |
| B点（最左端） | A点に同じ | A点に同じ | A点に同じ | - a | ka | A点に同じ |
EA = KA + UA = 0 + \(\large{\frac{1}{2}}\)ka2 = \(\large{\frac{1}{2}}\)ka2
A点（＝B点）でのおもりの速さは vA = (vB) = 0 です。往復運動の最端では、おもりの動きは一瞬止まります。
EX = KX + UX = \(\large{\frac{1}{2}}\)mvx2 + \(\large{\frac{1}{2}}\)kx2
力学的エネルギー保存の法則より EX = EA ですので、
\(\large{\frac{1}{2}}\)m vx2 + \(\large{\frac{1}{2}}\)kx2 = \(\large{\frac{1}{2}}\)ka2
∴ mvx2 + kx2 = ka2
∴ mvx2 = ka2 - kx2
∴ vx2 = \(\large{\frac{k}{m}}\)(a2 - x2)
∴ vx = \(\sqrt{\frac{k}{m}(a^2-x^2)}\)
EO = KO + UO = \(\large{\frac{1}{2}}\)mvO2 + 0 = \(\large{\frac{1}{2}}\)mvO2
力学的エネルギー保存の法則より EO = EA ですので、
\(\large{\frac{1}{2}}\)mvO2 = \(\large{\frac{1}{2}}\)ka2
∴ m vO2 = ka2
∴ vO2 = a2\(\large{\frac{k}{m}}\)
∴ vO = a\(\sqrt{\large{\frac{k}{m}}}\)
A点に同じ
力学的エネルギー保存の法則を使うことにより、水平ばね振り子の各点でのおもりの速さが求められます。
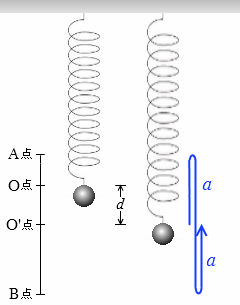ばね定数 k [N/m] のばねの上端を固定し、下端に質量 m [kg] のおもりを付けたばね振り子を、鉛直に吊るして静止させます。このとき自然長からの伸びが d [m] であるとすると、重力（mg）と弾性力（kd）がつり合っているのだから、mg = kd であります。さらにこの位置から a [m] だけ引き上げて離すと、つり合いの位置を中心にして、振幅 a [m] の往復運動をします。つり合いの位置O'点からおもりの任意の位置までの変位を y [m] とします。重力による位置エネルギーの基準点は自然長のO点とします。
各点での力学的エネルギーを求めた後、おもりの速さを求めてみます。
| 力学的エネルギー | 運動エネルギー | 重力による 位置エネルギー | 弾性エネルギー | O点からの変位 | 弾性力 | O'点からの 変位 | 弾性力+重力 | 速さ | |
|---|---|---|---|---|---|---|---|---|---|
| A点（最上端） | EA | KA = 0 | U重A = mg(a - d) | U弾A = \(\large{\frac{1}{2}}\)k(a - d)2 | a - d | - k(a - d) | a | - k(a - d) - mg = - k(a - d) - kd = - ka | vA = 0 |
| Y点（任意の位置） | EY | KY = \(\large{\frac{1}{2}}\)mvy2 | U重Y = mg(y - d) | U弾Y = \(\large{\frac{1}{2}}\)k(y - d)2 | y - d | - k(y - d) | y | - k(y - d) - mg = - k(y - d) - kd = - ky | vy |
| O点（自然長） | EO | KO = \(\large{\frac{1}{2}}\)mvO2 | U重O = 0 | U弾O = 0 | 0 | 0 | d | 0 - mg = - kd | vO |
| O'点（つり合いの位置） | EO' | KO' = \(\large{\frac{1}{2}}\)mvO'2 | U重O' = mg(- d) | U弾O' = \(\large{\frac{1}{2}}\)kd2 | - d | - k(- d) = kd | 0 | kd - mg = kd - kd = 0 | vd |
| B点（最下端） | EB | KB = 0 | U重B = mg(-a-d) | U弾B = \(\large{\frac{1}{2}}\)k(a+d)2 | - a - d | - k(- a - d) = k(a + d) | - a | k(a + d) - mg = k(a + d) - kd = ka | vB = 0 |
EA = KA + U重A + U弾A
= 0 + mg(a - d) + \(\large{\frac{1}{2}}\)k(a - d)2
= mga - mgd + \(\large{\frac{1}{2}}\)k(a2 - 2ad + d2)
= mga - mgd + \(\large{\frac{1}{2}}\)ka2 - kad + \(\large{\frac{1}{2}}\)kd2 mg = kd を代入して
= mga - mgd + \(\large{\frac{1}{2}}\)ka2 - mga + \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd ……①
EY = KY + U重Y + U弾Y
= \(\large{\frac{1}{2}}\)mvy2 + mg(y - d) + \(\large{\frac{1}{2}}\)k(y - d)2
= \(\large{\frac{1}{2}}\)mvy2 + mg(y - d) + \(\large{\frac{1}{2}}\)k(y2 - 2yd + d2)
= \(\large{\frac{1}{2}}\)mvy2 + mgy - mgd + \(\large{\frac{1}{2}}\)ky2 - kyd + \(\large{\frac{1}{2}}\)kd2 mg = kd を代入して
= \(\large{\frac{1}{2}}\)mvy2 + mgy - mgd + \(\large{\frac{1}{2}}\)ky2 - mgy + \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 - \(\large{\frac{1}{2}}\)mgd ……②
EO = KO + U重O + U弾O
= \(\large{\frac{1}{2}}\)mvO2 + 0 + 0
= \(\large{\frac{1}{2}}\)mvO2 ……③
EO' = KO' + U重O' + U弾O'
= \(\large{\frac{1}{2}}\)mvO'2 + mg(-d) + \(\large{\frac{1}{2}}\)kd2 mg = kd を代入して
= \(\large{\frac{1}{2}}\)mvO'2 - mgd + \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)mvO'2 - \(\large{\frac{1}{2}}\)mgd ……④
EB = KB + U重B + U弾B
= 0 + mg(- a - d) + \(\large{\frac{1}{2}}\)k(a + d)2
= - mga - mgd + \(\large{\frac{1}{2}}\)k(a2 + 2ad + d2)
= - mga - mgd + \(\large{\frac{1}{2}}\)ka2 + kad + \(\large{\frac{1}{2}}\)kd2 mg = kd を代入して
= - mga - mgd + \(\large{\frac{1}{2}}\)ka2 + mga + \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd ……⑤
この式は①式と同じです。
力学的エネルギー保存の法則より EA = EY = EO = EO' = EB です。
つまり、①式 = ②式 = ③式 = ④式 = ⑤式 です。
\(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 - \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)mvO2
= \(\large{\frac{1}{2}}\)mvO'2 - \(\large{\frac{1}{2}}\)mgd
= \(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd
です。
③式以外の各式をよく見ますと - \(\large{\frac{1}{2}}\)mgd という項が共通しています。m も g も d もはじめに定めた定数ですので - \(\large{\frac{1}{2}}\)mgd は定数であり、一定です。
ですので、この項を打ち消すために各式に \(\large{\frac{1}{2}}\)mgd を加えても、等式が成り立ちます。
それぞれ計算しますと、
\(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)ka2 ……①'
= \(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 - \(\large{\frac{1}{2}}\)mgd + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 ……②'
= \(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)mgd ……③'
= \(\large{\frac{1}{2}}\)mvO'2 - \(\large{\frac{1}{2}}\)mgd + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)mvO'2 ……④'
= \(\large{\frac{1}{2}}\)ka2 - \(\large{\frac{1}{2}}\)mgd + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)ka2 ……⑤'
これらの式を上で説明した水平ばね振り子の場合と見比べると、これはO'点を中心とした水平ばね振り子の力学的エネルギーとみなすことができることがわかります。
| 水平ばね振り子 | 鉛直ばね振り子 |
|---|---|
| \(\large{\frac{1}{2}}\)ka2 | \(\large{\frac{1}{2}}\)ka2 |
| \(\large{\frac{1}{2}}\)mvx2 + \(\large{\frac{1}{2}}\)kx2 | \(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 \(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)mgd |
| \(\large{\frac{1}{2}}\)mvO2 | \(\large{\frac{1}{2}}\)mvO'2 |
| \(\large{\frac{1}{2}}\)ka2 | \(\large{\frac{1}{2}}\)ka2 |
（ \(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)mgd というのは mg = kd を代入すると \(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)kd2 です。）
つまり、
鉛直のばね振り子は、自然長を中心としてではなく、つり合いの位置を中心とした水平のばね振り子
とみなすことができます。本項で一番言いたいのはコレです。補足ページ、『ばね振り子』項の『自然長の位置を原点にとると』もご参照ください。
①'式 = ②'式 = ③'式 = ④'式 = ⑤'式 であることを利用して各点でのおもりの速さを求めてみます。
A点でのおもりの速さは vA = 0 です。自明です。
②'式 = ①'式 だから
\(\large{\frac{1}{2}}\)mvy2 + \(\large{\frac{1}{2}}\)ky2 = \(\large{\frac{1}{2}}\)ka2
∴ mvy2 + ky2 = ka2
∴ mvy2 = ka2 - ky2
∴ vy2 = \(\large{\frac{k}{m}}\)(a2 - y2)
∴ vy = \(\sqrt{\frac{k}{m}(a^2 - y^2)}\)
y = 0 のとき、（つまりこれはO'点のとき）
vy = \(\sqrt{\frac{k}{m}(a^2 - 0^2)}\) = a\(\sqrt{\large{\frac{k}{m}}}\)
であり、下で示す vO' の値と一致します。
y = a のとき、（つまりこれはA点のとき）
vy = \(\sqrt{\frac{k}{m}(a^2 - a^2)}\) = 0
であり、上で示した vA の値と一致します。
③'式 = ①'式 だから
\(\large{\frac{1}{2}}\)mvO2 + \(\large{\frac{1}{2}}\)mgd = \(\large{\frac{1}{2}}\)ka2
∴ mvO2 + mgd = ka2
∴ vO2 + gd = \(\large{\frac{ka^2}{m}}\)
∴ vO2 = - gd + \(\large{\frac{ka^2}{m}}\)
∴ vO = \(\sqrt{-gd + \large{\frac{ka^2}{m}}}\) （補足ページ参照）
a = d のとき、
vO = \(\sqrt{-gd + \large{\frac{ka^2}{m}}}\)
= \(\sqrt{-gd + \large{\frac{kd^2}{m}}}\) mg = kd を代入して
= \(\sqrt{-gd + \large{\frac{mgd}{m}}}\)
= \(\sqrt{-gd - gd}\)
= 0
d = 0 のときは、
vO = \(\sqrt{-gd + \large{\frac{ka^2}{m}}}\)
vO = \(\sqrt{0 + \large{\frac{ka^2}{m}}}\)
vO = a\(\sqrt{\large{\frac{k}{m}}}\)
しかし実際には d = 0 となることはありません。おもりを付けて鉛直に吊るせば必ずばねは伸びるので。
④'式 = ①'式 だから
\(\large{\frac{1}{2}}\)mvO'2 = \(\large{\frac{1}{2}}\)ka2
∴ vO'2 = \(\large{\frac{ka^2}{m}}\)
∴ vO' = a\(\sqrt{\large{\frac{k}{m}}}\)
この値はY点でのおもりの速さの y = 0 の場合と一致します。また、水平ばね振り子におけるO点でのおもりの速さにも一致します。
B点でのおもりの速さはA点と同じく vB = vA = 0 です。
鉛直のばね振り子を、自然長を中心としてではなく、つり合いの位置を中心とした水平のばね振り子とみなす、つまり重力による位置エネルギーが無いとみなして、力学的エネルギーの式を立てることにより、各地点のおもりの速さを求めることができます。計算が楽になるということです。