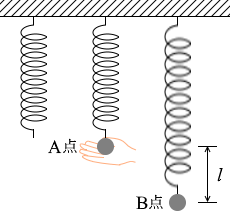
自然の長さの位置をA点、最大に伸びた位置をB点、求める最大の伸びを l と置きます。
自然の長さの位置を位置エネルギーの基準とし、各点での力学的エネルギーを求めます。
（A点での力学的エネルギー）=（A点での運動エネルギー）+（A点での重力による位置エネルギー）+（A点での弾性エネルギー）
= ( 0 ) + ( 0 ) + ( 0 )
= 0 ……①
（B点での力学的エネルギー）=（B点での運動エネルギー）+（B点での重力による位置エネルギー）+（B点での弾性エネルギー）
= ( 0 ) + ( - mgl ) + ( \(\large{\frac{1}{2}}\)kl2 )
= - mgl + \(\large{\frac{1}{2}}\)kl2 ……②
力学的エネルギー保存の法則により ① = ② であるから、
0 = - mgl + \(\large{\frac{1}{2}}\)kl2 ……③
∴ \(\large{\frac{1}{2}}\)kl2 = mgl
∴ \(\large{\frac{1}{2}}\)kl = mg
∴ l = \(\large{\frac{2mg}{k}}\)
と求められます。
（この問題は『鉛直ばね振り子の力学的エネルギー』において a = d の場合、といえます。）
（余談：もし手を離しておもりが静止した場合の話でしたら）
静止したときの伸びを d と置きますと、弾性力と重力がつり合っているのだから、
kd = mg
∴ d = \(\large{\frac{mg}{k}}\)
と求められます。
これを上の l = \(\large{\frac{2mg}{k}}\) と比べますと半分になっています。
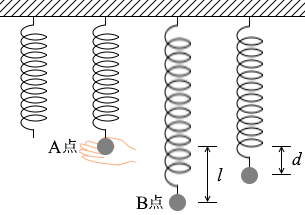手を離して静止した位置が、ばね振り子の往復運動の中心の位置になるのです。