小球の質量を m 、重力加速度の大きさを g 、衝突直前の速さを vA 、衝突直後の速さを vB とします。
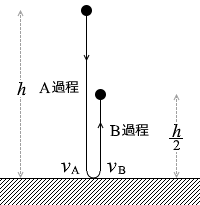
スタート地点から衝突直前までの過程をA過程と名付けると、A過程の力学的エネルギーは mgh です。これはA過程におけるどの地点でも変わらず mgh です。つまり、衝突直前の運動エネルギーも mgh です。
衝突直後から次の最高点までの過程をB過程と名付けると、B過程の力学的エネルギーは mg\(\large{\frac{h}{2}}\) です。これはB過程におけるどの地点でも変わらず mg\(\large{\frac{h}{2}}\) です。つまり、衝突直後の運動エネルギーも mg\(\large{\frac{h}{2}}\) です。
よって、
\(\large{\frac{衝突直後の運動エネルギー}{衝突直前の運動エネルギー}}\) = \(\large{\frac{mg\frac{h}{2}}{mgh}}\) = \(\large{\frac{1}{2}}\) [倍]
また、衝突直前の運動エネルギーは mgh なのだから、
mgh = \(\large{\frac{1}{2}}\)mvA2
∴ vA2 = 2gh
∴ vA = \(\sqrt{2gh}\)
一方、衝突直後の運動エネルギーは mg\(\large{\frac{h}{2}}\) なのだから、
mg\(\large{\frac{h}{2}}\) = \(\large{\frac{1}{2}}\)mvB2
∴ vB2 = gh
∴ vB = \(\sqrt{gh}\)
よって、
\(\large{\frac{衝突直後の速さ}{衝突直前の速さ}}\) = \(\large{\frac{\sqrt{gh}}{\sqrt{2gh}}}\) = \(\large{\frac{1}{\sqrt{2}}}\) [倍]
(別解)
力学的エネルギー保存の法則を忘れてしまった場合には、等加速度直線運動の時間を含まない式
v2 - v02 = 2ax
を使って解きます。
(A過程、下向き正)
vA2 - 02 = 2gh
∴ vA = \(\sqrt{2gh}\)
運動エネルギーは
\(\large{\frac{1}{2}}\)mvA2 = \(\large{\frac{1}{2}}\)m × 2gh = mgh
(B過程、上向き正)
02 - vB2 = 2(-g)\(\large{\frac{1}{2}}\)h
∴ vB = \(\sqrt{gh}\)
運動エネルギーは
\(\large{\frac{1}{2}}\)mvB2 = \(\large{\frac{1}{2}}\)m × gh = \(\large{\frac{1}{2}}\)mgh
よって、
\(\large{\frac{衝突直後の運動エネルギー}{衝突直前の運動エネルギー}}\) = \(\large{\frac{\frac{1}{2}mgh}{mgh}}\) = \(\large{\frac{1}{2}}\) [倍]
\(\large{\frac{衝突直後の速さ}{衝突直前の速さ}}\) = \(\large{\frac{\sqrt{gh}}{\sqrt{2gh}}}\) = \(\large{\frac{1}{\sqrt{2}}}\) [倍]
(余談)
ちなみに、このときの反発係数は \(\large{\frac{1}{\sqrt{2}}}\) です。