図1のように、ばね定数 k の軽いばねを天井からつり下げ、質量 m の小物体を、手で下からばねに押し当て、ばねを自然の長さから鉛直上向きに d だけ縮めた。この状態から小物体を支える手を離すと、重力とばねの力により、小物体は初速度 0 で鉛直下向きに運動し始めた。小物体は、ばねが自然の長さに達した後に、ばねから離れて、落下運動を続けた。重力加速度の大きさを g とする。
（問1）ばねが自然の長さに達した瞬間の小物体の運動エネルギーを式で表わせ。
（問2）小物体を支える手を離した後の小物体の運動を考える。図1に示す小物体の位置から小物体が運動した距離 x と、加速度の大きさとの関係を表すグラフとして最も適当なものを、次の①～⑥のうちから一つ選べ。
#センター12本試
（問1）
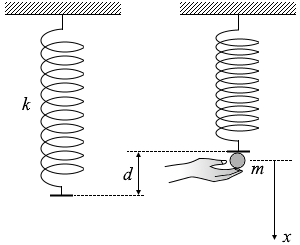
自然長の位置を位置エネルギーの基準とすると、d だけ持ち上げられた位置での小物体の力学的エネルギーは
（運動エネルギー）+（位置エネルギー）+（弾性エネルギー）= 0 + mgd + \(\large{\frac{1}{2}}\)kd2
求める運動エネルギーを K と置くと、自然長の位置での小物体の力学的エネルギーは
（運動エネルギー）+（位置エネルギー）+（弾性エネルギー）= K + 0 + 0
力学的エネルギー保存の法則より上の2式は等しいから、
0 + mgd + \(\large{\frac{1}{2}}\)kd2 = K + 0 + 0
∴ K = mgd + \(\large{\frac{1}{2}}\)kd2
（問2）
もし自由落下であれば常に g の加速度で運動していきますので、
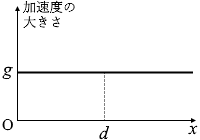グラフはこのようになりますが、
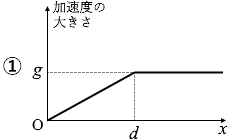
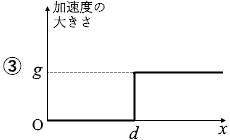
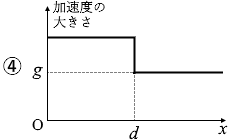
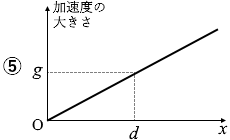
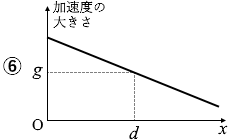
x が 0 から d までの間は弾性力が加わりますので、加速度は g より大きくなります。弾性力というのは自然長からの距離が遠いほど大きくなるのですから、x が 0 のときが一番大きくて、d のときが一番小さくなります。
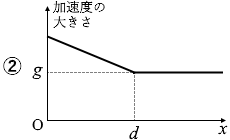このようなことを表しているグラフは ② です。
（運動方程式を立てて加速度の式を求めてみる）
0 ≦ x ≦ d の間は、小物体には重力と弾性力がはたらきます。重力の大きさは mg で、弾性力の大きさは k(d - x) です。
加速度を a 、鉛直下向きを正として運動方程式を立てますと、
ma = mg + k(d - x)
∴ a = g + \(\large{\frac{k}{m}}\)d - \(\large{\frac{k}{m}}\)x
この方程式が表すグラフは切片が g + \(\large{\frac{k}{m}}\)d で、傾きが - \(\large{\frac{k}{m}}\) です。x が d のときに a が g になります。
x > d においては、小物体には重力しかはたらかないので、
ma = mg
∴ a = g
となります。
（余談：自然長の位置以外で小物体がばねと離れることがあり得るのか）
ばね定数 k や小物体の質量 m を大きくしたり小さくしたりしても、自然長の位置以外で小物体がばねと離れることはありません。
ばねの質量を m' 、ばねの先端の加速度を a' 、ばね定数を k' 、自然長からの伸びを l として、ばねの運動方程式を無理矢理立てると、
m'a' = k'l
となりますが、高校物理ではばねの質量 m' は無限小とみなしますので（本問の問題文の「軽いばね」というのは質量無限小のばねという意味です）、上式より、a' が無限大になってしまい、この値が g より小さくなるようなことはありません。また、l = 0 では a' = 0 になってしまい、つまり自然長の位置では加速度がピタリと無くなってしまいます。
というわけで、ばねと小物体は必ず自然長の位置で離れます。
あくまでも理想上の話です。