氷の上で石を滑らせることについて考えよう。はじめ、図1のように、質量 M の人が質量 m の石とともに、速度 V0 で摩擦のない水平な氷の上を滑っている。ただし、すべての運動は一直線上で起こるとし、図1・図2の右向きを正の向きとする。
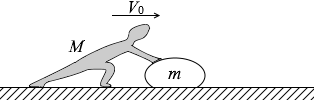
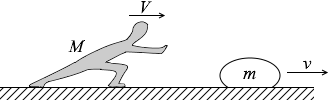
（問1）
（問2）qG7F9
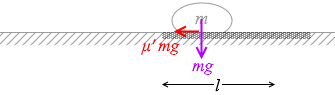
（問3）石が人と離れて速度 v となった後、石はあらい面の場所に来てまもなく静止した。静止するまでにあらい面のところを滑った距離はいくらか。ただし、石とあらい面の間の動摩擦係数を μ' 、重力加速度の大きさを g とする。
#センター00本試
石の運動エネルギーは \(\large{\frac{1}{2}}\)mv2 です。静止すれば石の運動エネルギーは 0 です。この差分は、摩擦力がした仕事（摩擦熱）によって失われたと考えられます。
石には mg の重力が掛かり、垂直抗力は mg であるので、摩擦力は μ'mg です。静止するまでに滑った距離を l と置きますと、摩擦力がした仕事は
μ'mg × l
です。
これが運動エネルギーの差分と考えられますので、
\(\large{\frac{1}{2}}\)mv2 - 0 = μ'mg × l
∴ \(\large{\frac{1}{2}}\)v2 = μ'g × l
∴ l = \(\large{\frac{v^2}{2μ'g}}\)
となります。