あらい斜面をすべり下りる物体の運動

変数を定義

非保存力がはたらく運動の例として、摩擦のあるあらい斜面をすべり下りる物体の運動を取り上げてみます。

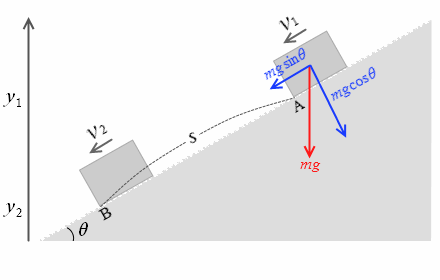水平面との角度を θ、物体と斜面との間の動摩擦係数を μ'、物体の質量を m、A点における速さを v₁、高さを y₁、B点における速さを v₂、高さを y₂、すべった距離を s とします。

摩擦力がした仕事 W

まず、摩擦力がした仕事 W を求めます。

摩擦力がした仕事 W　というのは　- 摩擦力 × 移動距離 s　です。

摩擦力　というのは　動摩擦係数 μ' × 垂直抗力　です。

垂直抗力　というのは　mgcosθ　です。

つまり、
摩擦力がした仕事 W = - 摩擦力 × 移動距離 s
　　　　　　　　　 = - 動摩擦係数 μ' × 垂直抗力 × 移動距離 s
　　　　　　　　　 = - μ' × mgcosθ × s
　　　　　　　　　 = - μ'mgscosθ
です。

ΔE = W の式

次に、力学的エネルギーの差分は非保存力のした仕事であるという ΔE = W の式を立ててみます。

　　ΔE = E_B - E_A = ( K_B + U_B ) - ( K_A + U_A ) = W

　∴　(\(\large{\frac{1}{2}}\)mv₂² + mgy₂) - (\(\large{\frac{1}{2}}\)mv₁² + mgy₁) = - μ'mgscosθ　　……①

エネルギーの原理の式

次に、エネルギーの原理の式を立ててみます。

このときの物体にされた仕事というのは摩擦力がした仕事だけではありません。そもそも物体がすべり下りるのは重力のせいです。重力も物体に対して仕事をしているのです。エネルギーの原理の式においては保存力である重力がした仕事も考慮に入れなければなりません。

重力のした仕事を W_重 とすると、

　　W_重 = 重力の運動方向成分 × 移動距離 s

　　　　= mgssinθ　　（『斜面上の運動』参照）

　　　　= mg(y₁ - y₂)　　（∵ ssinθ = y₁ - y₂ 。『仕事の原理』参照）

よってエネルギーの原理の式は、

　　\(\large{\frac{1}{2}}\)mv₂² - \(\large{\frac{1}{2}}\)mv₁² = （重力がした仕事 W_重）+（摩擦力がした仕事 W）

　　　　　　　　　　 = mg(y₁ - y₂) - μ'mgscosθ　　……②

　∴　\(\large{\frac{1}{2}}\)mv₂² - \(\large{\frac{1}{2}}\)mv₁² - mg(y₁ - y₂) = - μ'mgscosθ

　∴　(\(\large{\frac{1}{2}}\)mv₂² + mgy₂) - (\(\large{\frac{1}{2}}\)mv₁² + mgy₁) = - μ'mgscosθ　　……③

となり、③式は①式とまったく同じになります。つまり、ΔE = W と エネルギーの原理 は同じことを意味しているのです。

速さ v₂

次に、B点での物体の速さ v₂ を求めてみます。②式において右辺第一項の mg(y₁ - y₂) を mgssinθ に戻した式から求めてみます。

　　\(\large{\frac{1}{2}}\)mv₂² - \(\large{\frac{1}{2}}\)mv₁² = mgssinθ - μ'mgscosθ

　∴　\(\large{\frac{1}{2}}\)v₂² - \(\large{\frac{1}{2}}\)v₁² = gssinθ - μ'gscosθ

　∴　\(\large{\frac{1}{2}}\)v₂² - \(\large{\frac{1}{2}}\)v₁² = gs(sinθ - μ'cosθ)

　∴　　v₂² - v₁² = 2gs(sinθ - μ'cosθ)

　∴　　v₂² = v₁² + 2gs(sinθ - μ'cosθ)

　∴　　v₂ = \(\sqrt{{v_1}^2+2gs(\sin\theta-\mu'\cos\theta)}\)

式の中に m が含まれてないので、速さは物体の質量に無関係であることがわかります。（『落下の速さ』 参照。）

動摩擦角

さらに、上式の \(\sqrt{\ \ \ }\) の中の第ニ項　2gs(sinθ - μ'cosθ)　が 0 になった場合、

　　v₂ = \(\sqrt{{v_1}^2+0}\) = v₁

となります。v₂ = v₁ ということは速さが同じ、つまり一定の速さで斜面をずり落ちていくということです。

　　　　2gs(sinθ - μ'cosθ) = 0

　∴　　sinθ - μ'cosθ = 0

　∴　　μ'cosθ = sinθ

　∴　　μ' = \(\large{\frac{\sin\theta}{\cos\theta}}\)

　∴　　μ' = tanθ

これはつまり、 tanθ の値が動摩擦係数 μ' の値と一致するように角度をとると、すべり落ちる物体の速さが一定になるということです。摩擦角と似ています。あちらを静止摩擦角と呼ぶことにすれば、こちらは動摩擦角とでも呼ぶことができます（正式名称ではありません）。

y₂ を基準

最後に念のため、
実際に問題を解くときは、ここでの y₂ を 0 、つまり y₂ を基準面として y₁ の高さだけを考える方が計算が楽になります。ここでは説明のため y₂ ≠ 0 としました。