図1のように、斜面S0、S1と水平な床がなめらかにつながっている。斜面S0および床は摩擦のない面であり、斜面S1は粗い面である。床から高さ h の斜面S0上の点Pより、質量 m の小物体Aを斜面に沿って下方に速さ v0 で打ち出したところ、床に置かれた質量 M の小物体Bに衝突した。ただし、斜面S1の水平面からの角度を θ とし、重力加速度の大きさは g とする。また、斜面S1と小物体Bの間の動摩擦係数を μ' とする。
（問1）小物体Bに衝突する直前の小物体Aの速さ v1 はどれだけか。
（問2）小物体Aは小物体Bに衝突した直後に静止した。衝突直後の小物体Bの速さ v2 はどれだけか。
（問3）図2のように、小物体Bは斜面S1をのぼり、点Qにおいて速さが 0 になった。点Qの床からの高さはいくらか。
#センター03本試
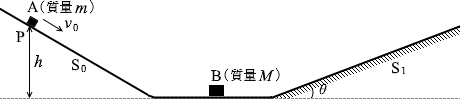
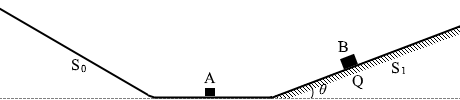
（問1）
小物体Aの点Pにおける力学的エネルギーは
\(\large{\frac{1}{2}}\)mv02 + mgh ……①
小物体Aの衝突直前の力学的エネルギーは
\(\large{\frac{1}{2}}\)mv12 + mg×0 ……②
力学的エネルギー保存の法則より ① = ② であるから、
\(\large{\frac{1}{2}}\)mv12 = \(\large{\frac{1}{2}}\)mv02 + mgh
∴ v12 = v02 + 2gh
∴ v1 = \(\sqrt{{v_0}^2+2gh}\)
と求まります。
（問2）
2物体の衝突直前の運動量の和は
mv1 + M×0 ……③
2物体の衝突直後の運動量の和は
m×0 + Mv2 ……④
運動量保存の法則より ③ = ④ であるから、Mv2 = mv1
∴ v2 = \(\large{\frac{m}{M}}\)v1
（問3）図2のように、小物体Bは斜面S1をのぼり、点Qにおいて速さが 0 になった。点Qの床からの高さはいくらか。
求める高さを h1 と置きます。
小物体Bの斜面S1をのぼり始める直前の力学的エネルギーは
\(\large{\frac{1}{2}}\)Mv22 + Mg×0 ……⑤
小物体Bの点Qでの力学的エネルギーは
\(\large{\frac{1}{2}}\)M×0 + Mgh1 ……⑥
摩擦がはたらいているので力学的エネルギーは保存されません。摩擦が無ければもっと高くまでのぼっていたはずです。力学的エネルギー⑥は力学的エネルギー⑤より小さくなっています。その差分は摩擦力にされた仕事です。摩擦熱です。つまり、
⑤ - ⑥ = (摩擦力にされた仕事）
⇔ \(\large{\frac{1}{2}}\)Mv22 - Mgh1 = (摩擦力にされた仕事） ……⑦
です。
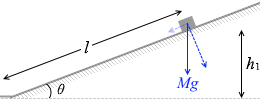摩擦力にされた仕事というのは、（摩擦力）×（移動距離）で、
（摩擦力）というのは（動摩擦係数）×（垂直抗力）で、
（垂直抗力）は Mgcosθ で、
（移動距離）は l = \(\large{\frac{h_1}{\sinθ}}\) で、
つまり、
（摩擦力にされた仕事）= μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\)
です。
よって、⑦式は
\(\large{\frac{1}{2}}\)Mv22 - Mgh1 = μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\) ……⑦'
となります。
これは、
始めに \(\large{\frac{1}{2}}\)Mv22 のエネルギーがあって、摩擦力が - μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\) の仕事をして、Mgh1 のエネルギーになった（摩擦力が仕事をしなければもっと高くまでのぼって Mgh2 とかになっていた）と考えれば、
\(\large{\frac{1}{2}}\)Mv22 - μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\) = Mgh1
と立式することもできますし、
始めにあった \(\large{\frac{1}{2}}\)Mv22 のエネルギーが、摩擦熱 μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\) と位置エネルギー Mgh1 に変わった、と考えれば、
\(\large{\frac{1}{2}}\)Mv22 = μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\) + Mgh1
と立式することもできます。
いずれも同じ式です。
⑦'式を解きます。
\(\large{\frac{1}{2}}\)Mv22 - Mgh1 = μ'Mgcosθ×\(\large{\frac{h_1}{\sinθ}}\)
∴ \(\large{\frac{1}{2}}\)v22 - gh1 = μ'gcosθ×\(\large{\frac{h_1}{\sinθ}}\)
∴ v22sinθ - 2gh1sinθ = 2μ'gh1cosθ
∴ v22sinθ = 2gh1sinθ + 2μ'gh1cosθ
∴ 2gh1(sinθ + μ'cosθ) = v22sinθ
∴ h1 = \(\large{\frac{{v_2}^2\sinθ}{2g(\sinθ + μ'\cosθ)}}\)