運動量保存の法則

運動量保存の法則

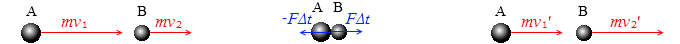
質量 m₁ 、速度 v₁ の物体Aと、質量 m₂ 、速度 v₂ の物体Bが同じ直線上を運動していて衝突し、速度がそれぞれ v₁' 、v₂' になったとします。

このとき、物体Aが物体Bにおよぼした力を F とすると、作用⋅反作用の法則により、物体Bが物体Aにおよぼしたした力は - F です。そして物体Aが物体Bに力をおよぼした時間を Δt とすると当然物体Bが物体Aに力をおよぼした時間も Δt です。よって、物体Aが物体Bにおよぼした力積は FΔt で、物体Bが物体Aにおよぼした力積は - FΔt です。

このことを式で表すと、

　　物体Aについて　：　m₁v₁' - m₁v₁ = - FΔt　　……①

　　物体Bについて　：　m₂v₂' - m₂v₂ = FΔt　　……②

この２式から FΔt を消去すると、

　　　　- ( m₁v₁' - m₁v₁ ) = m₂v₂' - m₂v₂

　∴　　m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'　　……③

となり、物体Aと物体Bの運動量の和は衝突の前後で変わらないことが分かります。

このことを運動量保存の法則といいます。

①式、②式は運動方程式（運動の第2法則）から導き出されたものでした。そしてこれら２式から③式を導き出したのは F が共通であることからであり、これは作用⋅反作用の法則（運動の第3法則）によるものです。つまり、運動量保存の法則は、運動の第2法則と運動の第3法則から導き出されたものといえます。＊逆に、運動量保存の法則こそが本質的なもので、そこから導き出されるのが運動の第2法則と運動の第3法則である、という考え方もあります。
　閉じる

もし作用⋅反作用の法則以外の力がはたらいてしまうと、運動量保存の法則は成り立ちません。作用⋅反作用の法則の力というのは物体系＊物理では複数の物体をひとまとめにして物体系と呼びます。
　閉じるの内力＊物体系内の物体同士が互いにおよぼし合う力のことです。
　閉じるのことで、作用⋅反作用の法則以外の力というのは、物体系の外力＊物体系の外からおよぼされる力のことです。
　閉じるのことです。外力がはたらいてしまう場合は運動量保存の法則は成り立たないのです＊現実世界では空気抵抗などの外力が僅かにでもはたらいてしまうので厳密には運動量保存の法則は成り立ちません。運動量保存の法則は空気抵抗などを無視したときの理想の話です。
　閉じる。

ここまで説明したことは力や速度がベクトルであっても成り立つことなので、③式を書き直すと以下のようになります。

平面運動における運動量保存の法則

m₁\(\vec{v_1}\) + m₂\(\vec{v_2}\) = m₁\(\vec{v_1}\)' + m₂\(\vec{v_2}\)'　を図で表現すると以下のようになります。

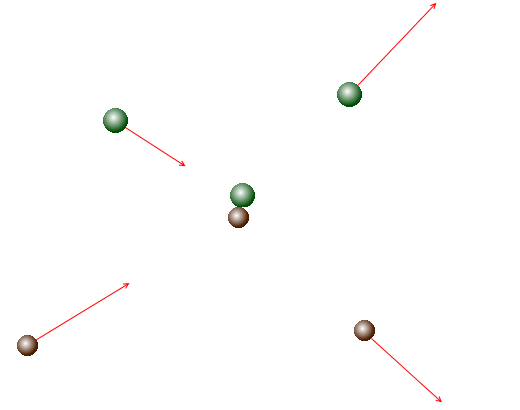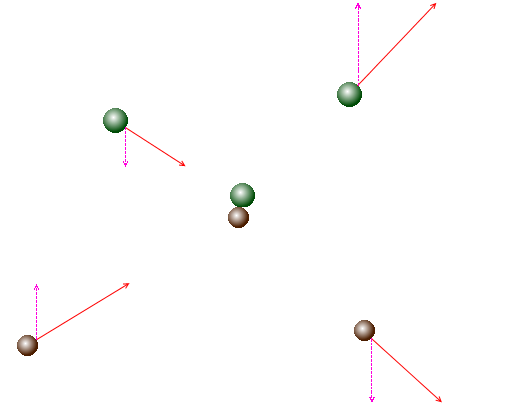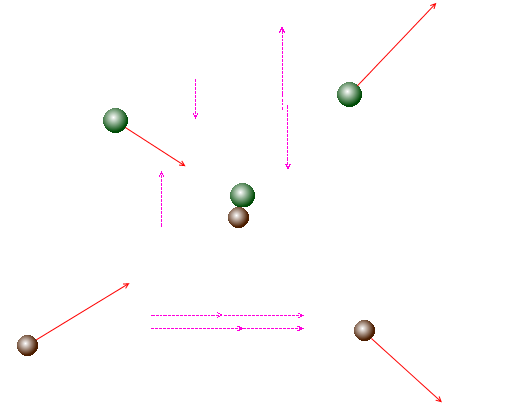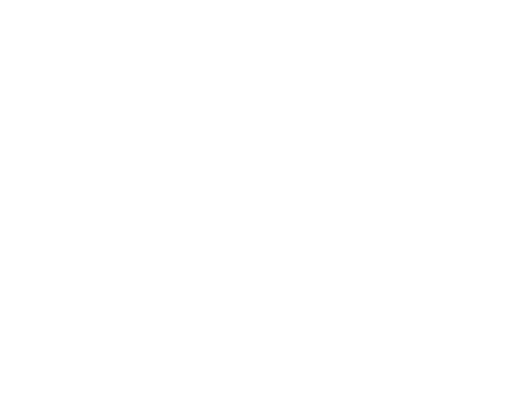
また、ベクトルは x軸と y軸に分解することができるので上式は以下のように書くことができます。

　　　　m₁v_1x + m₂v_2x = m₁v_1x' + m₂v_2x'

　　　　m₁v_1y + m₂v_2y = m₁v_1y' + m₂v_2y'

これを図で表現すると以下のようになります。