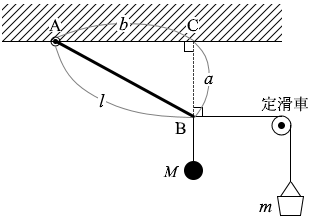
長さ l の軽い棒の一端を自由に回転できる支点Aで水平な天井に取り付け、他端Bには2本の軽い糸をつける。一方の糸には質量 M のおもりをつり下げ、他方の糸には砂を入れた容器をなめらかに回る定滑車を通してつり下げる。砂の量を調整して容器と砂の質量の和を m にしたとき、図6のように糸は水平になり棒が静止した。点Bから天井に引いた垂線と天井の交点を点Cとし、ACの距離を b 、BCの距離を a とする。M と m の関係を表す式として正しいものを、下の①~⑥のうちから一つ選べ。
① Ml = ma ② Ma = mb ③ Mb = ml ④ Ml = mb ⑤ Ma = ml ⑥ Mb = ma
#センター14本試
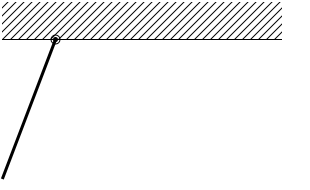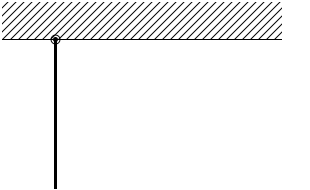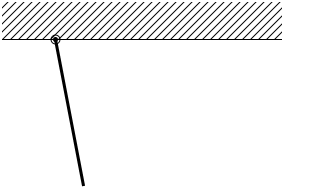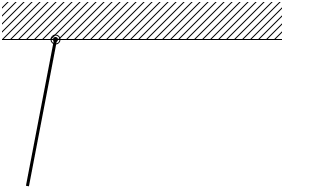 自由に回転できる支点を持つ棒を
自由に回転できる支点を持つ棒を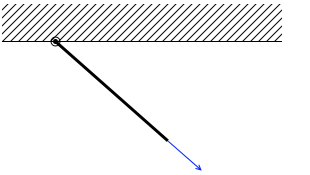 引っ張れば、棒は必ず力の方向を向くはずです。
引っ張れば、棒は必ず力の方向を向くはずです。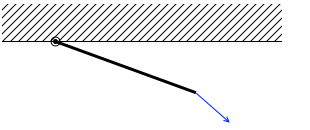 違う方向を向くことはありえません。(今は棒は軽いとされています。軽いというのは質量が 0 とみなせるということです。)
違う方向を向くことはありえません。(今は棒は軽いとされています。軽いというのは質量が 0 とみなせるということです。)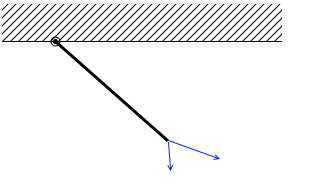 例えば2つの力がはたらいていれば、
例えば2つの力がはたらいていれば、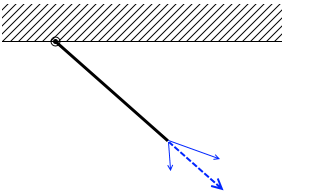 その
その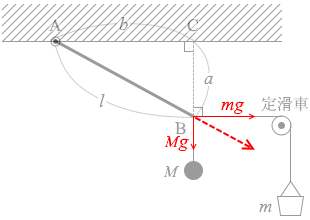 本問では、鉛直方向に Mg の力が、水平方向に mg の力が
本問では、鉛直方向に Mg の力が、水平方向に mg の力が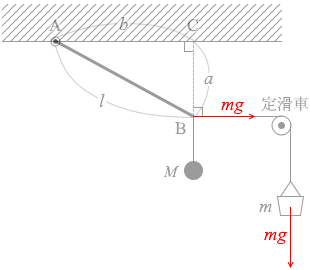
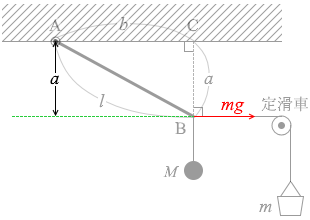 mg による
mg による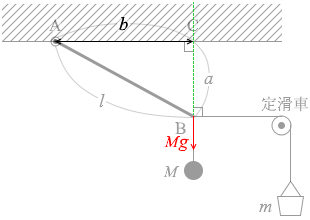 Mg による力のモーメントの大きさは
Mg による力のモーメントの大きさは