図1は、ある小物体にはたらいている力 \(\vec{F_1}\) 、\(\vec{F_2}\) の向きと大きさを、方眼を用いて表したものである。この小物体にはたらく合力の x成分 Fx と、y成分 Fy の値はいくらか。ただし、方眼の1目盛りは大きさ 1N の力に対応している。
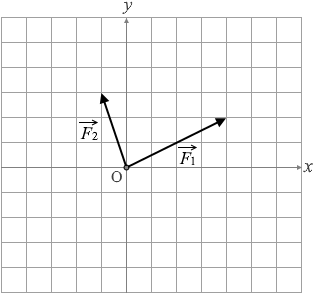
#センター16本試物理基礎
図1は、ある小物体にはたらいている力 \(\vec{F_1}\) 、\(\vec{F_2}\) の向きと大きさを、方眼を用いて表したものである。この小物体にはたらく合力の x成分 Fx と、y成分 Fy の値はいくらか。ただし、方眼の1目盛りは大きさ 1N の力に対応している。
#センター16本試物理基礎
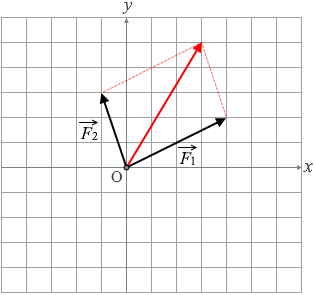力はベクトルであり、力を合成するにはベクトルの加法にならえば良いから、合力は左図の赤矢印のようになり、
x成分を読み取ると、Fx = 3 [N]
y成分を読み取ると、Fy = 5 [N]
となります。
成分ごとに足して、
Fx = 4 + (-1) = 3 [N]
Fy = 2 + 3 = 5 [N]
と考えてもいいです。
（発展）
\(\vec{F_1}\) - \(\vec{F_2}\) は？と問われれば、
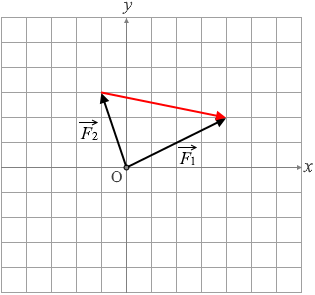\(\vec{F_2}\) の先端から \(\vec{F_1}\) の先端へ矢印を引いて、
Fx = 5 [N]
Fy = - 1 [N]
です。
これを
Fx = 4 [N]
Fy = 2 [N]
などとしてはダメです。
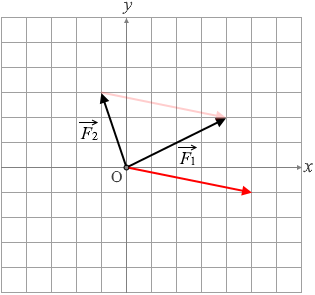ベクトルの根元を原点に持ってこなければいけません。ベクトルというものはどっちの向きにどのくらいの大きさであるのかを表す量です。
この計算を成分ごとに考えるとすれば、
Fx = 4 - (-1) = 5 [N]
Fy = 2 - 3 = - 1 [N]
となります。