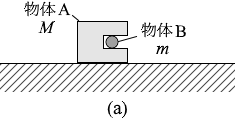
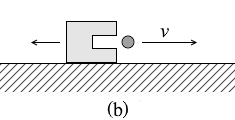
図4(a)のように、なめらかで水平な床の上で、質量 M の物体Aと質量 m の物体Bが一体となって静止している。物体Aから物体Bを打ち出したところ、図4(b)のように、物体Bは速さ v で水平方向に動き出した。動き出した直後の、物体Aに対する物体Bの相対速度の大きさを式で表わせ。
#センター16本試物理
図4(a)のように、なめらかで水平な床の上で、質量 M の物体Aと質量 m の物体Bが一体となって静止している。物体Aから物体Bを打ち出したところ、図4(b)のように、物体Bは速さ v で水平方向に動き出した。動き出した直後の、物体Aに対する物体Bの相対速度の大きさを式で表わせ。


#センター16本試物理
一体となって静止しているときの運動量の和は
M⋅0 + m⋅0
動き出した直後の物体Aの速度を V (V < 0) とすると、運動量の和は
M⋅V + m⋅v
運動量保存の法則より上の2式は等しいから、
M⋅0 + m⋅0 = M⋅V + m⋅v
∴ - M⋅V = m⋅v
∴ V = - \(\large{\frac{m}{M}}\)v
v - V = v - (- \(\large{\frac{m}{M}}\)v) = v + \(\large{\frac{m}{M}}\)v = \(\large{\frac{M+m}{M}}\)v