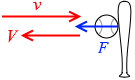
始めにボールが飛んできた方向を正とします。
そうしますと、飛んできた速度（ v ）と飛んで行った速度（ - V ）の差は
- V - v
であり、力を受けていた間の平均の加速度の大きさを a としますと、
a = \(\large{\frac{-V-v}{⊿t}}\)
です。
よって、ボールが受けた平均の力の大きさを F として、この運動 ボールとバットが接触している短い間の運動です。 における運動方程式を立てますと、
ma = - F
⇔ m\(\large{\frac{-V-v}{⊿t}}\) = - F ……※
∴ F = \(\large{\frac{m(V+v)}{⊿t}}\)
となります。
（運動量の変化と力積の関係）
上の※式の両辺に ⊿t を掛けて
m(- V) - mv = - F⊿t
とすると、運動量の変化と力積の関係を表す式になります。