J字形をした断面積一定の管があり、管の壁は熱をよく通す。大気圧 p0 の下で、その管に液体を注入し、図4(a)に示すように、管の上端の一方をふたでふさいだ。このとき、ふたにより閉じ込められた気体の圧力は p0 、温度は T0 、鉛直方向の長さは l0 であった。この状態を状態Aとする。ただし、液体の密度を ρ 、重力加速度の大きさを g とする。また、液体の蒸発は無視できるとし、大気圧 p0 、液体の密度 ρ は常に一定であるとする。
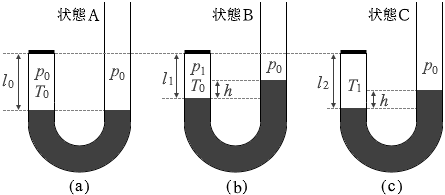
（問5）さらに液体を注いだところ、液面が上昇し、図4(b)のように、気体部分の長さが l1 、液面の高さの差が h になった。温度は T0 のまま変わらなかった。この状態を状態Bとする。状態Bの気体の圧力 p1 を式で表せ。
（問6）\(\large{\frac{p_1}{p_0}}\)を表す式として正しいものを、次の①～⑥のうちから一つ選べ。
① \(\large{\frac{l_0}{h}}\) ② \(\large{\frac{l_0}{l_1}}\) ③ \(\large{\frac{h}{l_1}}\) ④ \(\large{\frac{h}{l_0}}\) ⑤ \(\large{\frac{l_1}{l_0}}\) ⑥ \(\large{\frac{l_1}{h}}\)
（問7）しばらくして外気温が変化し、液面の高さが変わったので、高さの差が状態Bと同じ h になるように液体の量を調整した。その結果、図4(C)のような状態Cになった。このとき、気体の温度は外気温と同じT1 であった。状態Cの気体部分の長さ l2 を l1 を用いて表す式として正しいものを、次の①～⑥のうちから一つ選べ。
① \(\large{\frac{T_0}{T_1}}\)l1 ② \(\large{\frac{T_1}{T_0}}\)l1 ③ \(\large{\frac{T_0}{T_1-T_0}}\)l1 ④ \(\large{\frac{T_1-T_0}{T_0}}\)l1 ⑤ \(\large{\frac{T_1}{T_1-T_0}}\)l1 ⑥ \(\large{\frac{T_1-T_0}{T_1}}\)l1
#センター14本試
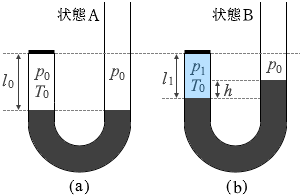圧力 p1 というのは左図の水色部分の圧力のことであり（本問においては、気体に関してはその圧力は高さに依らず、液体に関してはその圧力は高さに依る、ということが前提になっています）、その圧力は
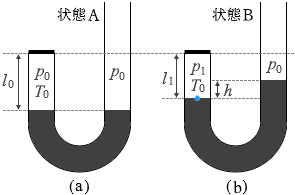左図の水色地点の圧力のことであり、
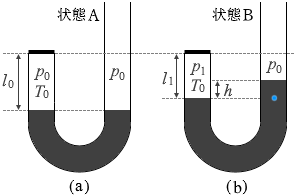左図の水色地点の圧力のことでもあります。
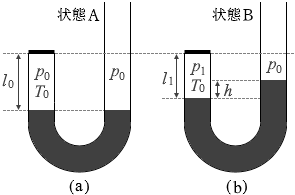管の断面積の大きさを S とおいて、
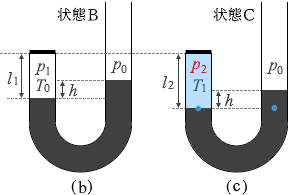閉じ込められた気体の圧力を p2 としますと、問5と同じように考えて、