図1のように、熱をよく通す二つの容器A、Bが、コックのついた容積の無視できる細い管でつなげられ、大気中におかれている。容器A、Bの容積はそれぞれ VA 、VB である。コックが閉じた状態で、同じ分子からなる理想気体を、容器A、Bにそれぞれ物質量 nA 、nB だけ閉じ込める。大気の温度は常に一定であるものとする。
（問1）容器A、B内の気体の圧力をそれぞれ pA 、pB としたとき、圧力の比 \(\large{\frac{p_A}{p_B}}\) を式で表わせ。
（問2）次に、コックを開ける。十分に時間がたったとき、容器内の気体の圧力 p を式で表わせ。
（問3）コックを開ける前の気体の内部エネルギーの和 U0 と、コックを開けて十分に時間がたった後の内部エネルギー U1 の差 U0 - U1 を式で表わせ。
#センター16本試物理
（問1）
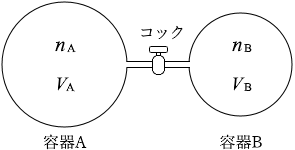
容器は熱をよく通すということだから大気と容器A内の気体と容器B内の気体は温度が同じであり、この温度を T と置きます。また、気体定数を R と置きます。すると理想気体の状態方程式より、
pAVA = nART ……①
pBVB = nBRT ……②
①式を②式で割りますと、
\(\large{\frac{p_{\rm{A}}V_{\rm{A}}}{p_{\rm{B}}V_{\rm{B}}}}\) = \(\large{\frac{n_{\rm{A}}}{n_{\rm{B}}}}\)
∴ \(\large{\frac{p_{\rm{A}}}{p_{\rm{B}}}}\) = \(\large{\frac{n_{\rm{A}}V_{\rm{B}}}{n_{\rm{B}}V_{\rm{A}}}}\)
（問2）
コックを開くと容器A内の圧力と容器B内の圧力は等しくなります。この圧力を p と置きます。
また、コックを開くと容器A内の物質量と容器B内の物質量が変化します。この物質量を nA' 、nB' と置きます。しかし物質量の総量は変化しません。物質量とは分子の個数のことです。分子は二つの容器を行き来するかもしれませんが容器から外に漏れるようなことはありません。よって、
nA' + nB' = nA + nB ……③
です。
さらに、温度は両容器内とも T のままです。
これらを踏まえて、十分に時間が経って管を移動する分子の動きがおさまった状態での各容器内の気体の状態方程式を立てますと、
pVA = nA'RT ……④
pVB = nB'RT ……⑤
上の③式の両辺に RT を掛けまして、
nA'RT + nB'RT = nART + nBRT
①式、②式、④式、⑤式を代入しますと、
pVA + pVB = pAVA + pBVB
∴ p = \(\large{\frac{p_{\rm{A}}V_{\rm{A}}+p_{\rm{B}}V_{\rm{B}}}{V_{\rm{A}}+V_{\rm{B}}}}\)
（問3）
理想気体の内部エネルギーは、物質量と絶対温度のみに比例します
単原子分子でなくてもそうです。
。コックを開ける前と後で物質量も温度も変化しません。よって内部エネルギーは変化せず、
U0 - U1 = 0
（分子が漏れたり足されたりしなければ、内部エネルギーと温度は実質的に同じものとみなせます。）