内部エネルギー

内部エネルギーとは

ある1つの物体に着目したときに、その物体の運動エネルギーと位置エネルギーとの和を力学的エネルギーといいます。

物体というものは分子（あるいは原子）で構成されていて、その分子は動いている（運動エネルギーがある）し、分子と分子の間には力がはたらいている（位置エネルギーがある＊ 分子間に力がはたらくとすると、その距離の大小によって位置エネルギーがあるとみなせます。『重力による位置エネルギー』、『弾性力による位置エネルギー』、『静電気力による位置エネルギー』参照。 閉じる ）ので、個々の分子には力学的エネルギーがある、といえます。しかし、何万、何億という個数の分子をひとまとめにしてみたときには、それらの分子の力学的エネルギーのことを内部エネルギーと呼びます。

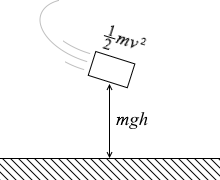：物体の力学的エネルギー = \({\large\frac{1}{2}}mv^2 + mgh\)

：物体の内部エネルギー = 物体を構成する分子のエネルギー

この内部エネルギーは上の力学的エネルギーとは関連性はありません。内部エネルギーを考えるときは、物体内部のエネルギーのことだけを考えます。物体の速さや物体の高さのことは考えません。＊ 領域内のことだけを考えて領域外のことを考えないとき、この領域のことを「系」といいます。大学物理の用語です。『慣性系⋅非慣性系』参照。 閉じる

単原子分子の理想気体の内部エネルギー

理想気体では、分子間力は無いものとみなすので、分子間力による位置エネルギーは無いと考えます。よって、分子の運動エネルギー（=熱）の総和がそのまま理想気体の内部エネルギーとなります。

単原子分子の理想気体の分子1個の運動エネルギーは

　　　\({\large\frac{1}{2}}m\overline{{v}^2} = {\large\frac{3}{2}}kT = {\large\frac{3}{2}}⋅{\large\frac{R\ }{N_{\rm A}}}⋅T\)

であり、この分子の個数が 1mol あるとすると、つまり \(N_{\rm A}\)倍すると、

　　　\({\large\frac{1}{2}}m\overline{{v}^2}⋅N_{\rm A}\) = \({\large\frac{3}{2}}⋅{\large\frac{R\ }{1}}⋅T\)

であり、分子の個数が \(n\) [mol] あるとすると、さらに \(n\)倍して、

　　　\(n⋅{\large\frac{1}{2}}m\overline{{v}^2}⋅N_{\rm A} = n⋅{\large\frac{3}{2}}⋅{\large\frac{R\ }{1}}⋅T\)

であり、これを \(U\) [J] とおくと<＊ \(U\) の語源は分かりません 閉じる 、以下のようになります。

単原子分子の理想気体の内部エネルギーは、物質量（≒分子の個数）と絶対温度のみに比例します。物質の種類は無関係です。

物質量が一定（≒分子の個数が一定≒質量が一定）ならば、絶対温度が \(ΔT\) [K] 変化したときの内部エネルギーの変化量 \(ΔU\) [J] は以下のようになります。

　　　　\(ΔU = {\large\frac{3}{2}}nRΔT\)　＊ \(ΔU = {\large\frac{3}{2}}nR(T + ΔT) - {\large\frac{3}{2}}nRT = {\large\frac{3}{2}}nRΔT\) 閉じる