Pさんの家と消防署は、図3のように一直線の道路に沿って建っている。救急車がサイレンを鳴らしながら消防署を出発し、一定の速度で走行した後に停車する。サイレンは一定の振動数 f0 の音を出すとして、Pさんが家で聞く救急車のサイレンの音の振動数について考える。ただし、消防署とPさんの家で区切られる道路の三つの領域を、それぞれ図3のようにA、B、Cとする。
（問4）救急車が消防署を出発して、領域Aに停車した。このとき、Pさんの聞く音の振動数は時間とともにどうように変化するか。また領域Cに停車した場合はどうか。それぞれ最も適当なグラフを、次の①～④のうちから一つ選べ。
（問5）救急車は消防署を出発し、一定の速度で時間 T0 の間走行した後停車した。このときPさんが聞いたサイレンの音の振動数は図4のように時間変化した。図4において、振動数 f1 の音が聞こえていた時間 T1 は時間 T0 の何倍になるか。
#センター08本試
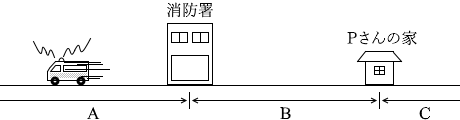
（問4）
（領域Aに停車した場合）
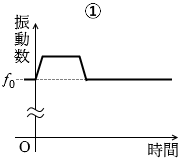
音源が遠ざかっていくとき、ドップラー効果により、音は低く聞こえます。音が低いということは振動数が小さいということです。
音源の移動が止まれば振動数は元に戻ります。
答えは ② です。
（領域Cに停車した場合）
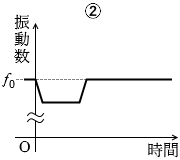
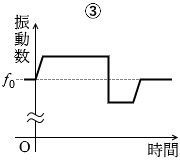
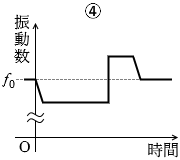
救急車が領域Bを走行する間は、音源が近づいてくるということであり、音が高く聞こえます。振動数が大きいということです。通り過ぎて領域Cを走行する間は、今度は音源が遠ざかっていくということであり、音が低く聞こえます。
Pさんが聞く音は、救急車が通り過ぎる瞬間に急激に高い音から低い音に変わります。
音源の移動が止まれば振動数は元に戻ります。
答えは ③ です。
救急車がこちらに向かってくるときはサイレンの音が高く聞こえ、通り過ぎたとたん音が低く聞こえるのは日常生活でも経験することです。そのことが分かっていればこの問題は解けます。ドップラー効果の公式は使いません。ドップラー効果というものがどういうものかを問う問題です。
（問5）
題意が読み取りにくいと思いますので説明します。
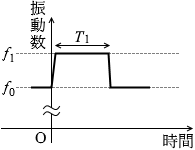
グラフによると、音が聞こえていた時間は振動数が大きくなっています。救急車はPさんに近づいてきたということです。振動数というのは 1秒間に媒質が往復する回数（＝ 1秒間に空気を揺らす回数）です。Pさんにとってはそれが大きくなった（音が高くなった）ように聞こえるのです。1秒間にPさんの鼓膜を揺らす回数が多くなったのです。
たとえば、救急車が停車していて、振動数 f = 3 [Hz] の（1秒当たり3回空気を揺らす）音を 2秒間出していたとすると、この音はPさんにとっても振動数 3Hz の音であり、聞こえる時間も 2秒間です。
しかし、救急車がPさんに近づいているとすると、波の間隔は縮み、Pさんの鼓膜を揺する振動数は 3Hz より大きくなります。たとえばPさんの鼓膜が感じる振動数が 4Hz だったとすると、Pさんが音を聞いていた時間は 2秒間より短くなり、2×\(\large{\frac{3}{4}}\) = 1.5 [秒間] となります。音波の進む速さは一定ですので、波の間隔が縮めば振動数は大きくなり、波が通過する時間は短くなります。このとき救急車が走行していた時間はあくまでも 2秒間であり、発する振動数は 3Hz です。しかしPさんが聞くサイレンの音は、1.5秒間で、4Hz なのです。
救急車が停車してしまえばPさんが聞く音は 3Hz に戻ります。
というわけで、Pさんが聞こえていた時間は T1 = \(\large{\frac{f_0}{f_1}}\) T0 です。
（別解）
振動数というものは 1秒間に何個波を作ったかという数値なので、振動数が f0 で、作っていた時間が T0 ということは、その間に作られた波の個数は f0T0 [個] です。上の例え話でいえば、振動数が 3Hz で、時間が 2秒間で、それによって作られた波の個数が 6個です。
この波の個数というものはPさんにとっても変わりません。上の例え話では、救急車にとっても、Pさんにとっても波の個数は 6個です。
ということは次の式が成り立ちます。
f0T0 = f1T1
∴ T1 = \(\large{\frac{f_0}{f_1}}\) T0