qH3DA　■わかりやすい高校物理の部屋■

　媒質中を伝わる波動を、ベルトコンベアによる物品の搬送と対応させて、ドップラー効果を考えてみよう。
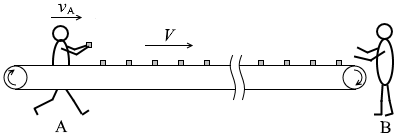
　図1のように十分に長いベルトコンベアがあり、上に乗せたものを一定の速さ V で右に運んでいる。左側にいる作業者Aは、一定の速さ v_A で作業者Bに向かって移動しながら、一定の時間間隔 T₀ で小さな箱をベルトコンベアの上に乗せていく。右側の作業者Bは、運ばれてくる箱をベルトコンベアの端で回収する。ただし、v_A < V とする。

（問1）次の文章中の空欄ア⋅イに入れる式の組合せとして正しいものを、下の①〜⑥のうちから一つ選べ。

　作業者Aが静止している場合（v_A = 0）はベルトコンベア上の箱の間隔は T₀V であるが、動いている場合（v_A ≠ 0）は、箱の間隔は d =アとなる。このとき、静止している作業者Bが箱を受け取る時間間隔は T =イである。

	ア	イ
①	`T`₀`V`	\(\large{\frac{d}{V+v_A}}\)
②	`T`₀`V`	\(\large{\frac{d}{V-v_A}}\)
③	`T`₀(`V` + `v`_A)	\(\large{\frac{d}{V}}\)
④	`T`₀(`V` + `v`_A)	\(\large{\frac{d}{V-v_A}}\)
⑤	`T`₀(`V` - `v`_A)	\(\large{\frac{d}{V}}\)
⑥	`T`₀(`V` - `v`_A)	\(\large{\frac{d}{V+v_A}}\)

（問2）次の文章中の空欄ウ〜オに入れる語の組合せとして最も適当なものを、下の①〜⑥のうちから一つ選べ。

　作業者A、Bをそれぞれ波源と観測者にみたてて、ドップラー効果との対応を考えてみよう。箱の位置を波の山の位置、作業者Aが箱をおく時間間隔 T₀ を波源での波の周期、箱の速さ V を波の速さをみなすと、ベルトコンベア上にならぶ箱の間隔 d は観測される波のウ、作業者Bが箱を受け取る時間間隔 T は観測される波の周期と解釈できる。
　波源が運動してドップラー効果が起きているときは、波のエは変わらず、オが変化する。ベルトコンベアの搬送は波動とは異なる現象であるが、上記のように考えると、ドップラー効果を理解することができる。

	ウ	エ	オ
①	波長	波長	振動数
②	波長	速さ	振動数
③	振動数	波長	振動数
④	波長	振動数	速さ
⑤	振動数	振動数	速さ
⑥	振動数	速さ	波長

#センター14本試

（問1）
ア
直感で T₀(V - v_A) とわかると思いますが、一応説明しますと、

T₀秒の間に起こること：　

n個目の箱が、置かれてから T₀秒間の間に進む距離は T₀V [m] 。（単位は架空）

n個目の箱を置いたあと、(n + 1)個目の箱を置くまでに、作業者Aは T₀v_A [m] だけ前進している。

よって、n個目の箱と (n + 1)個目の箱との距離は

　　　　T₀V - T₀v_A = T₀(V - v_A)

イ
m個目と (m + 1)個目との距離は d であり、(m + 1)個目の速さは V であるので、m個目が届いてから (m + 1)個目が届く時間は（\(\frac{距離}{速さ}\)=） \(\large{\frac{d}{V}}\) 。
（これは T₀ ではありません。T₀ はもうちょっと大きいです。T₀ だったものが \(\large{\frac{d}{V}}\) に小さくなったことがドップラー効果に例えられます。）

というわけで答えは ⑤ 。

（問2）
ウ　波長

エ
一貫して変わらないのはベルトコンベアの速さであり、これは波の速さに例えられます。『音源が動くと振動数が変わる』で説明したように、ドップラー効果が起きている最中でも波の速さは変わりません。風が吹いている場合など、よっぽどの例外があるとき以外は、ドップラー効果における波の速さは一定です。
（ベルトコンベアが動くことは風が吹くことには例えられません。ベルトコンベアの速さは音波の速さ（約340m/s）に例えられます。）

オ
変化するのは、箱の間隔（=波長）と作業者Bが箱を受け取る時間間隔 T です。T₀ だったはずのものが \(\large{\frac{d}{V}}\) に小さくなります。この時間間隔 T は波の周期と解釈することができます。そして、周期の逆数が振動数であり、周期が変化するなら 振動数 も変化します。周期が小さくなるとき振動数は大きくなり、振動数が大きくなるということはこれは単位時間当たりの作業者Bが受け取る箱の数が増えることに例えられます。
（v = fλ より、v が一定のとき λ が変化すれば f も変化する、と考えてもいいです。）

というわけで答えは ② 。