qH42A

図2のように二つの小さなスピーカーS1、S2を並べて置き、発振器につないだ。S1とS2からは同じ振動数の音波を発生させることができる。図2には、振動数 f0 の音波を同位相で発生させたときの、ある時刻でのS1とS2からのそれぞれの音波の波面を示してある。実線は波の山の位置を表し、破線は谷の位置を表している。ただし、音速は 340m/s とする。

図 2

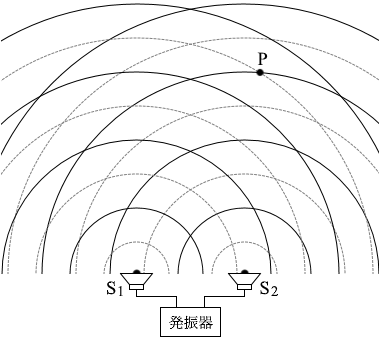
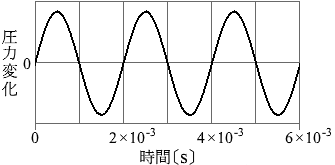
（問3）振動数 f0 の音波をS1だけから発生させた。このとき図2のP点での音波による空気の圧力変化を表したグラフが図3である。この音波の波長 λ の値はいくらか。

図 3

（問4）振動数 f0 の音波をS1とS2から同位相で発生させたとき、観測する場所によって音が強く聞こえたり、弱く聞こえたりした。これは、S1とS2から観測点までの距離の差(経路差)によって音波の干渉のようすが変わるためである。干渉によって音波が弱めあうときの経路差を表す式として正しいものを、次の①～④のうちから一つ選べ。ただし、λ は音波の波長であり、m = 0, 1, 2, ... である。

① \(\large{\frac{mλ}{2}}\)　　② \(\big(\)m+\(\large{\frac{1}{2}}\)\(\big)\)\(\large{\frac{λ}{2}}\)　　③ mλ　　④ \(\big(\)m+\(\large{\frac{1}{2}}\)\(\big)\)λ　　

　

（問5）次の文章中の空欄カ〜クの中に入れる語の組合せとして最も適当なものを、下の①～⑧のうちから一つ選べ。

　振動数 f0 の音波をS1とS2から同位相で発生させたとき、P点で音波はカあう。振動数を2倍にした音波（振動数 2f0 ）をS1とS2から同位相で発生させた場合はP点で音波はキあい、逆位相で発生させた場合はP点で音波はクあう。

カ キ ク
① 強め 強め 強め
② 強め 強め 弱め
③ 強め 弱め 強め
④ 強め 弱め 弱め
⑤ 弱め 強め 強め
⑥ 弱め 強め 弱め
⑦ 弱め 弱め 強め
⑧ 弱め 弱め 弱め

#センター11本試

（問3）
図3のグラフから読み取れるのは、波の1周期が 2×10-3 [s] ということです。そして、振動数というものは周期の逆数だから、

　　　　f0 = \(\large{\frac{1}{2×10^{-3}}}\) [Hz]

さらに、（v = fλ より）波長というものは速度を振動数で割ったものだから、

　　　　λ = \(\large{\frac{v}{f_0}}\) = 340 × 2×10-3 = 680×10-3 = 0.68 [m]

　

　

（問4）
波の干渉によって強めあうときの経路差は λ 、2λ 、3λ 、4λ 、… で、

弱めあうときの経路差は 0.5λ 、1.5λ 、2.5λ 、3.5λ 、… です。

つまり、弱めあうときの経路差を表す式は　④ \(\big(\)m+\(\large{\frac{1}{2}}\)\(\big)\)λ 　です。

　

　

（問5）
カ
P点では、S1から来た波が谷となっていて、S2から来た波が山となっているので、 弱めあい ます。

　

キ
振動数が2倍になるということは波の細かさが2倍になるということです。波の細かさが2倍になると、

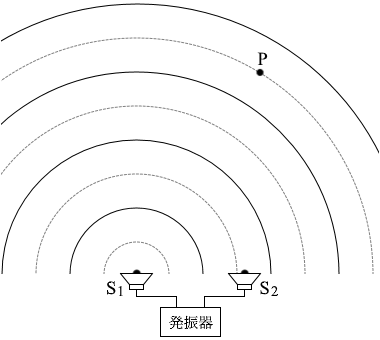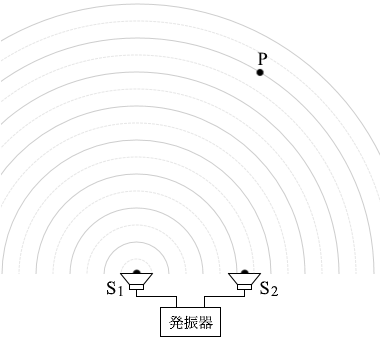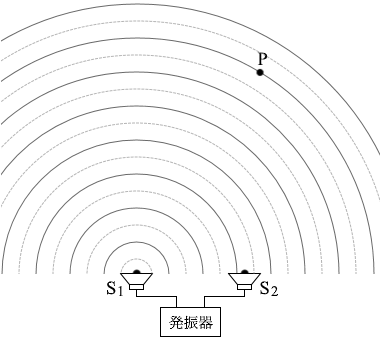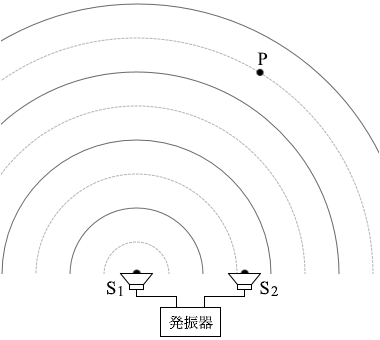S1から出た波はP点では、谷だったものが山になります。

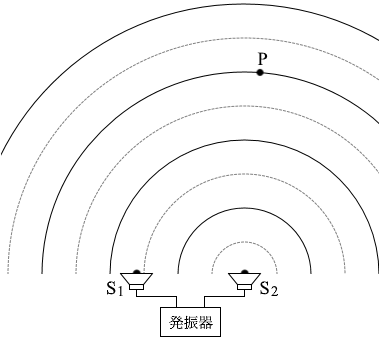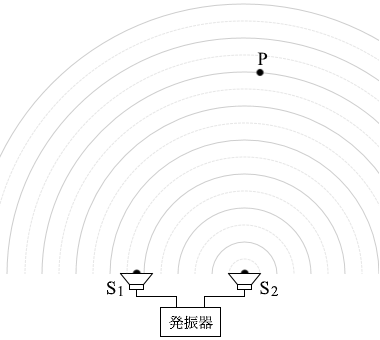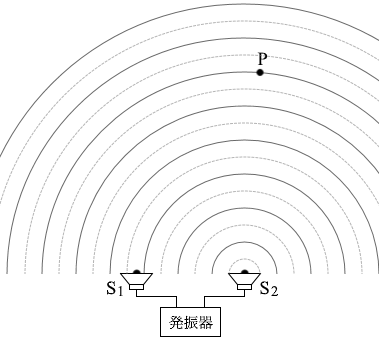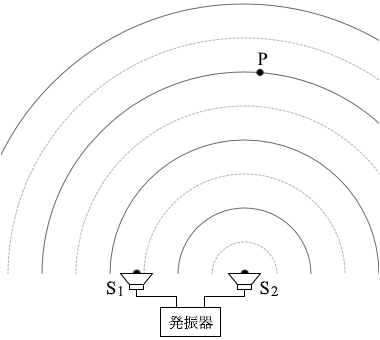S2から出た波はP点では、山だったものが山のままです。

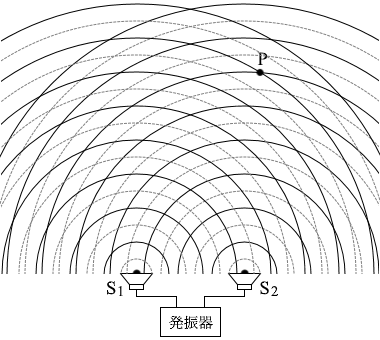つまり、P点では山と山のぶつかりあいとなり、 強めあい ます。

　

ク
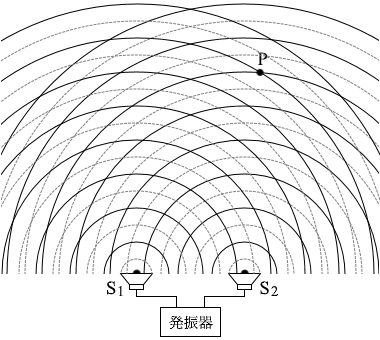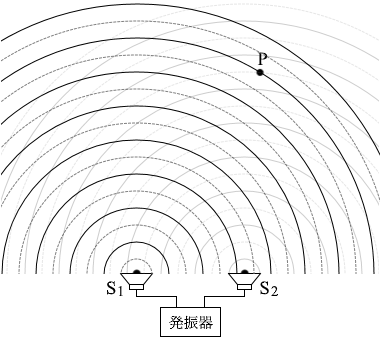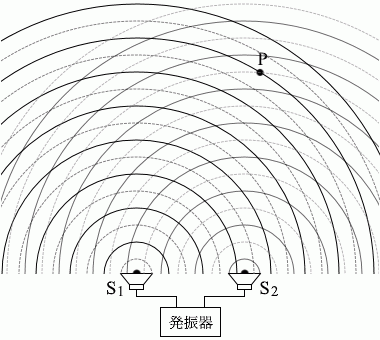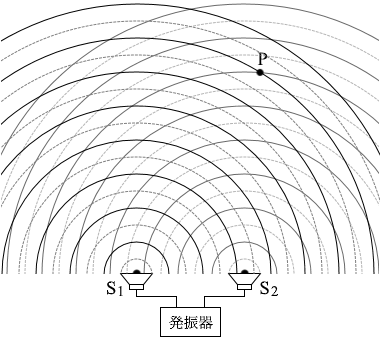S1とS2から音波を逆位相で発生させた場合は、P点では山と谷のぶつかりあいとなり、 弱めあい ます。

　

答は ⑥ です。

↑ ↓