qH18A

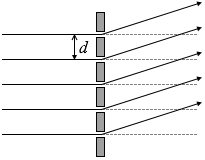
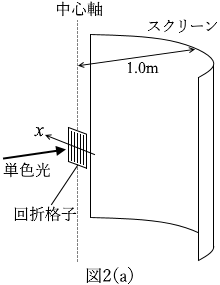
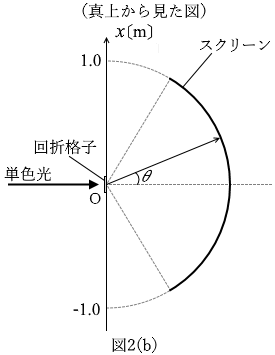
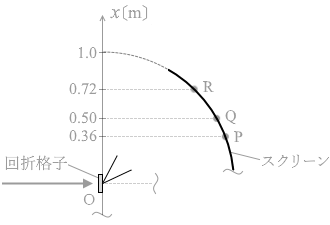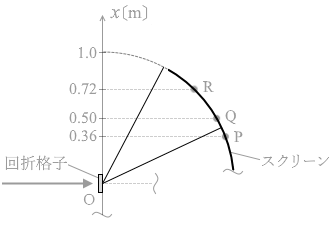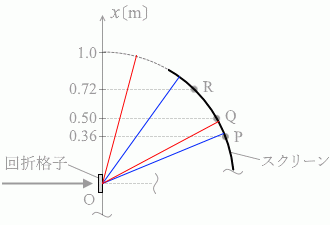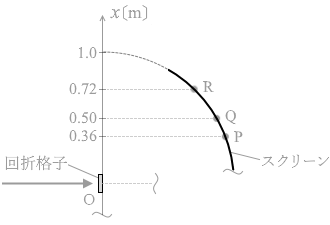
図1のように、スリットが間隔 d で並んだ回折格子に、単色光を垂直に入射させると、隣り合うスリットを通る光が強め合う方向に明線が生じる。図2(a)のように、半径 1.0m の円筒状のスクリーンを設置し、その中心軸上にスリットの向きと中心軸が平行になるように回折格子を置く。図2(b)は、図2(a)を真上から見た図である。図2(b)のように、回折格子に垂直に単色光を入射させ、入射光の進行方向と回折光の進行方向のなす角度を θ として、スクリーン上に現れる明線を - 60° < θ < 60° の範囲で観測する。回折格子の位置を原点Oとして、入射光および円筒の中心軸に垂直な方向に x軸を定める。

図 1
　

（問1）スリットの間隔 d が 1.2×10-6m の回折格子に、波長が 6.0×10-7m の単色光を入射させたとき、スクリーン上 (- 60° < θ < 60°) に現れる明線の数はいくつか。ただし、必要であれば sin60° ≒ 0.87 を用いてもよい。

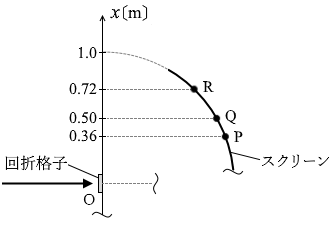
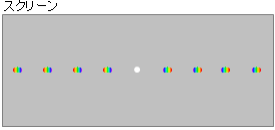
（問2）問1で使用した回折格子をとりはずし、スリットの間隔がわかっていない回折格子にとりかえる。この回折格子に、赤色の単色光と青色の単色光を同時に入射させたところ、スクリーンの 0° < θ < 60° の範囲には、図3のP、Q、Rの位置にのみ明線が観測された。3本の明線のうち、青色の明線はどれか。

図 3

#センター12本試

（問1）
回折格子の明線の条件の式 (dsinθ = mλ、mは整数) を立てますと、

　　　　1.2×10-6 × sinθ = m × 6.0×10-7

　∴　　1.2×10-6 × sinθ = m × 0.6×10-6

　∴　　1.2 × sinθ = m × 0.6

　∴　　m = 2 × sinθ　　……①

sin(-θ) = - sinθ 数学の教科書をご参照ください。 であり、- 60° < θ < 60° であるので、

　　　　- sin60° < sinθ < sin60°

sin60° ≒ 0.87 0.87 というのは \(\large{\frac{\sqrt{3}}{2}}\) のことです。 であるので、

　およそ　- 0.87 < sinθ < 0.87

①式より、

　およそ　- 2 × 0.87 < m < 2 × 0.87

　およそ　　- 1.74 < m < 1.74

m は整数だから、m = - 1, 0, 1

よって、スクリーン上に現れる明線は 3本 。

　

　

（問2）
『m次の干渉縞』の最後の所で説明しましたが、波長の短い青は内側に寄り、波長の長い赤は外側に寄ります。

スクリーンの範囲には3本しか明線がないということなので、内側のPから順に、青、赤、青です。

青色の明線は PとR です。

　

（余談）
青色の光の波長を λ青 と置いて、回折格子の明線の条件の式 (dsinθ = mλ) を立てますと、

　　　　dsinθ = mλ青

であり、m = 1 であれば、

　　　　dsinθ = λ青

となり、このときの sinθ が図の中で示された値 0.36 となっています。 単位円をご存知でしょうか。
数学の教科書の三角関数の所に載っているのですが、半径が 1 の円のことです。

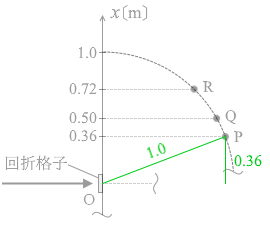sinθ = \(\large{\frac{0.36}{1.0}}\) = 0.36 です。

m = 2 の場合は、

　　　　dsinθ = 2λ青

であり、sinθ の部分も2倍になり、これが図の中の 0.72 という値のことです。

赤色の光の波長を λ赤 と置いて、明線の条件の式を立てれば、

　　　　dsinθ = mλ赤

となり、m = 1 のときの sinθ の値が図の中の 0.50 という値であり、m = 2 のときの sinθ の値が 1.0 という値です。

m が 3以上となる明線は無いわけですが、これは回折格子のスリットの間隔（格子定数）があまりにも小さい（細かい）からです。m は 2 までです。

『m次の干渉縞』では m が 4 まである図を示しましたが、これは格子定数が大きい（粗い）回折格子を用いたからです。

スリットの間隔が細かいと像は粗くなり、スリットの間隔が粗いと像は細かくなります。

↑ ↓