qI3G7

図1のように、空気中で平面ガラス板Aの一端を平面ガラス板Bの上に置き、Oで接触させた。Oから距離 L の位置に厚さ a の薄いフィルムをはさんで、ガラス板の間にくさび形のすきまを作り、ガラス板の真上から波長 λ の単色光を入射させた。ただし、空気に対するガラスの屈折率は 1.5 である。屈折率の小さい媒質を進んできた光が、屈折率の大きい媒質との境界面で反射するときは、位相が反転（π だけ変化）する。

図 1

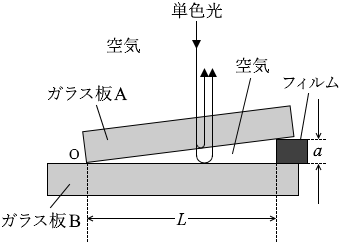
（問1）ガラス板の真上から観察したとき、ガラス板Aの下面で反射する光と、ガラス板Bの上面で反射する光とが干渉し、明線と暗線が並ぶ縞模様が見えた。隣り合う明線の間隔 d はいくらか。

　

（問2）次の文章中の空欄ア・イに入れる語と式の組合せとして最も適当なものを、下の①～⑥のうちから一つ選べ。

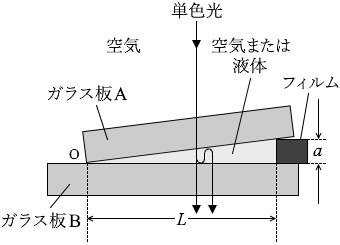
　ガラス板の真下から透過光を観測した。図2のように、反射せずに透過する光と、2回反射したのち透過する光とが干渉し、真上から見たとき明線のあった位置にはアが見えた。このとき、隣り合う明線の間隔は d であった。
　次に、空気に対する屈折率 n（ 1 < n < 1.5 ）の液体ですきまを満たしたところ、真下から見た隣り合う明線の間隔はイであった。

図 2
ア イ
① 明線 d
② 明線 nd
③ 明線 \(\large{\frac{d}{n}}\)
④ 暗線 d
⑤ 暗線 nd
⑥ 暗線 \(\large{\frac{d}{n}}\)

#センター17本試物理

（問1）
『くさび形空気層による光の干渉』において説明しましたが、明線と明線の間隔（Δx と置くと）は

　　　　Δx = \(\large{\frac{λ}{2\tanθ}}\)

です。

本問では Δx → d 、tanθ → \(\large{\frac{a}{L}}\) ですので、

　　　　 d = \(\large{\frac{λ}{2\frac{a}{L}}}\) = \(\large{\frac{Lλ}{2a}}\)

　

　

（問2）
ア
一応ことわっておきますが、「真上から見たとき明線のあった位置」というのは

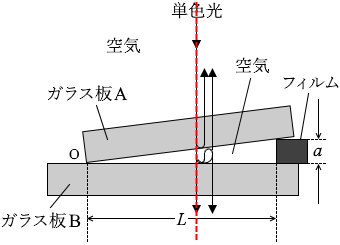左図の赤点線の位置、という意味です。

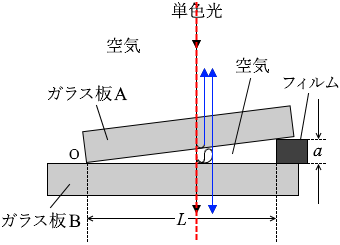左図の青色光線は分かりやすくするために右にズラして描いているだけで、本来は赤点線上にあります。

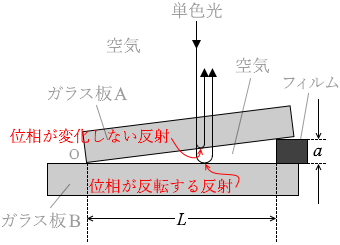この赤点線の位置を真上から見たときと真下から見たときで同じになるかそうでないのか、というのが問題の主旨です。

真上から見たときに見える光というのは、”位相が変化しない光”と”位相が反転した光”が干渉し合った光です。

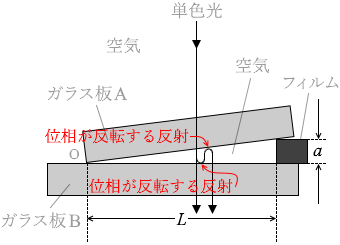一方、真下から見たときに見える光というのは、”位相が変化しない光”と”位相が2回反転した光”が干渉し合った光です。

つまり、真上から見たときと真下から見たときでは、明、暗が逆になります。

というわけで、真上から見たとき明線のあった位置を真下から見れば 暗線 が見えます。

　

イ
真上から見たときと真下から見たときでは、明線と暗線が反転するわけですが、反転しても線の間隔は変わるものではないので、これはつまり、明線の間隔は真上から見たときと真下から見たときで変わらないということです。

しかし、すきまの空気を液体に変えると光の波長が変わり（λ が \(\large{\frac{λ}{n}}\) になる たとえば屈折率が 1.5 の液体中では波長は \(\large{\frac{1}{1.5}}\)倍に小さくなります。 ）、問1で求めた明線の間隔の式

　　　　d = \(\large{\frac{Lλ}{2a}}\)

の λ の部分が \(\large{\frac{λ}{n}}\) になり、明線の間隔は

　　　　 \(\large{\frac{d}{n}}\)

となります。

　

答えは ⑥ です。

↑ ↓