qI819　■わかりやすい高校物理の部屋■

図1のように、一方の端をふたで閉じた細長い管が x軸に沿って置かれている。閉口端および開口端は、それぞれ x = 0 cm および x = 50 cm の位置にある。開口端近くに置かれたスピーカーから振動数 f₀ の音を発生させたところ共鳴した。このとき閉管内に定常波が生じ、x = 10 cm, 30 cm, 50 cm の3か所に腹ができていた。ただし、開口端補正は無視できるものとする。

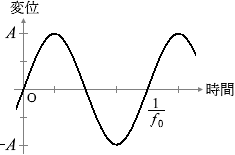
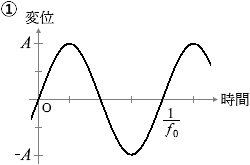
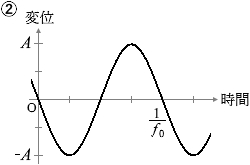
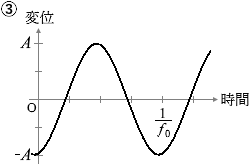
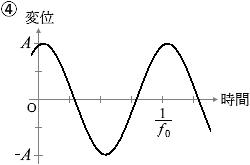
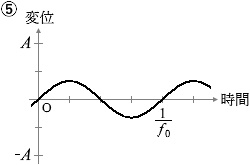
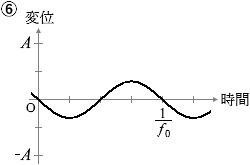
（問1）x = 10 cm における媒質の変位の時間変化は、図2のような振幅 A の正弦波で表される。x = 18 cm および x = 30 cm における媒質の変位の時間変化を表すグラフとして最も適当なものを、下の①～⑥のうちから一つずつ選べ。同じものを繰り返し選んでもよい。ただし、x軸の正の向きの変位を正とする。

（問2）図1の状態で閉管のふたを取ると共鳴しなくなった。そこで、スピーカーから発せられる音の振動数を f₀ から徐々に小さくしていくと、振動数が f₁ になったときに再び共鳴した。振動数の比 \(\large{\frac{f_1}{f_0}}\) として最も適当なものを、次の①～⑥のうちから一つ選べ。

①　\(\large{\frac{3}{5}}\)　　②　\(\large{\frac{2}{3}}\)　　③　\(\large{\frac{5}{7}}\)　　④　\(\large{\frac{4}{5}}\)　　⑤　\(\large{\frac{5}{6}}\)　　⑥　\(\large{\frac{6}{7}}\)　　

#センター16追試物理

（問1）
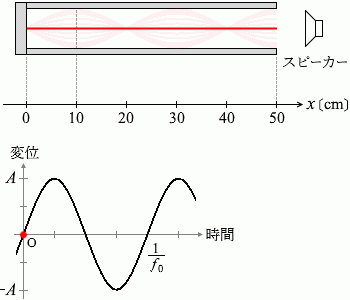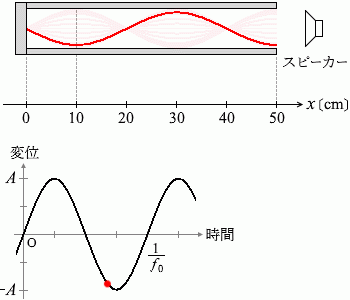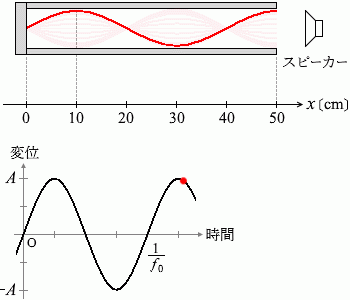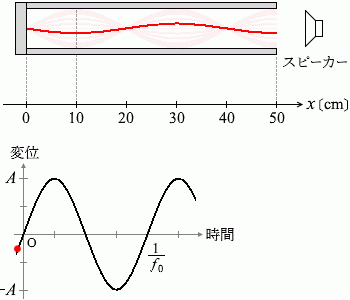x = 10 cm, 30 cm, 50 cm の3か所に腹ができていたということなので定常波の様子は左図のようになります。

図2のグラフは x = 10 cm の位置の波の揺れ方を表したものです。

x = 18 cm の位置の波の揺れ方を見てみますと、揺れ幅（振幅）は x = 10 cm の位置の揺れに比べ 1/3 くらいで、x = 10 cm の位置の揺れが最大のときに x = 18 cm の位置の揺れも最大になっているので、揺れのタイミング（位相）は同じであり、そのようなグラフは ⑤ です。

x = 30 cm の位置の波の揺れ方を見てみますと、揺れ幅（振幅）は x = 10 cm の位置と同じで、x = 10 cm の位置の揺れが最大のときに x = 30 cm の位置の揺れは最小（負）になっているので、揺れのタイミング（位相）は逆であり、そのようなグラフは ② です。

（余談:1）
x = 50 cm の位置の波の揺れ方は x = 10 cm の位置の揺れ方とまったく同じになっています。

（余談:2）
問題文に「ただし、x軸の正の向きの変位を正とする。」とありますが、これは音波というものが縦波であるということを意味しています。空気分子が右に動いたとき、グラフの変位が正、と定義しています。しかし問題を解く上で特に気にする必要はありません。

（問2）
ふたを取ると x = 0 cm の位置で波が反射（固定端反射）しなくなり定常波は崩れます（共鳴しなくなる）。そこで、音の振動数を徐々に小さくしていくとのことですが、これはすなわち波の波長を大きくしていくということです。空気中を伝わる波は速さが決まっていて（音速）、振動数と波長を掛けたものが速さであるので（v = fλ）、振動数を小さくしていくということは波長を大きくしていくということになります。

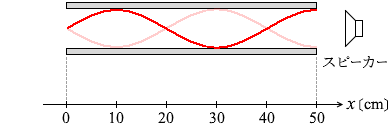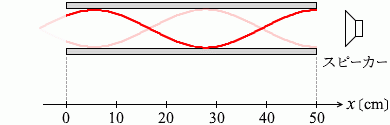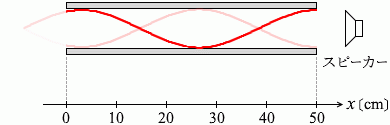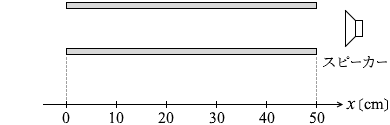波長を大きくしていくと、

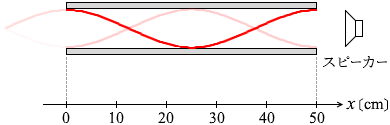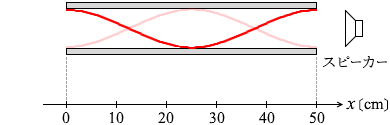左図のような形になったときに開管の2倍振動の定常波ができます（共鳴する）。このときの振動数が f₁ というわけです。

このときの波長は 50cm です。＊ 1波長の長さがどこからどこまでなのかは勘違いしやすいです。
気をつけてください。閉じる

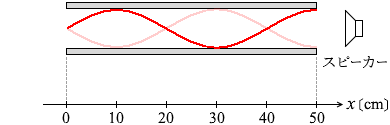波が f₀ のときの波長は 40cm です。

音速を V と置きますと、（v = fλ に代入して）

　　　　V = f₀ × 0.4

　　　　V = f₁ × 0.5

　∴　　\(\large{\frac{f_1}{f_0}}\) = \(\large{\frac{\frac{V}{0.5}}{\frac{V}{0.4}}}\) = \(\large{\frac{4}{5}}\)

答えは ④ です。