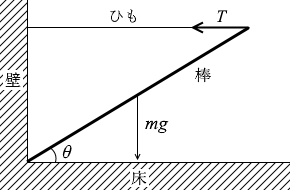
質量 m の一様な細い棒がある。図1のように棒の一端を水平な床と壁の隅につけ、他端を水平に張られたひもで引っ張り、棒が床となす角を θ に保つようにする。このとき、ひもの張力 T はいくらか。ただし、重力加速度の大きさを g とする。
#センター06本試
質量 m の一様な細い棒がある。図1のように棒の一端を水平な床と壁の隅につけ、他端を水平に張られたひもで引っ張り、棒が床となす角を θ に保つようにする。このとき、ひもの張力 T はいくらか。ただし、重力加速度の大きさを g とする。

#センター06本試
棒が床となす角を θ に保つということは、棒が動かないということであり、棒にはたらく力のモーメントがつり合っているということです。この力のモーメントの和(回転方向の力の和)について考えると張力 T の大きさが特定できます。水平方向の力の和や、鉛直方向の力の和は考えなくても大丈夫です。
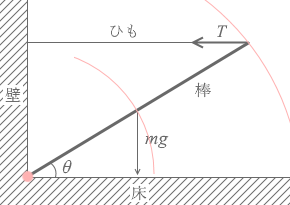 床と壁の隅を中心とした、棒にはたらく力のモーメントを考えます。
床と壁の隅を中心とした、棒にはたらく力のモーメントを考えます。
(力のモーメントの中心はどこに設定してもいいのですが、本問の場合は床と壁の隅を中心とするのが最も計算が楽です。床と壁の隅にはたらく力はどちら向きにどれだけ働いているかよくわかりません。よくわからない地点を中心としてしまえば、そこは力のモーメントの腕の長さが 0 なので計算する必要が無くなります。)
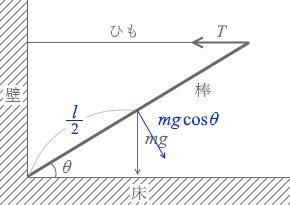 棒の長さを l としますと、
棒の長さを l としますと、
一様な棒の重心はその中点にあるので、重力 mg による力のモーメントは
mgcosθ × \(\large{\frac{l}{2}}\)
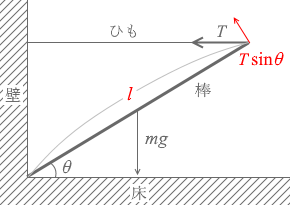 張力 T による力のモーメントは
張力 T による力のモーメントは
Tsinθ × l
この2つの力のモーメントがつり合っているのだから、
mgcosθ × \(\large{\frac{l}{2}}\) = Tsinθ × l ……①
mgcosθ × \(\large{\frac{l}{2}}\) - Tsinθ × l = 0
と立式してもいいです。
∴ T = \(\large{\frac{mg\cosθ}{2\sinθ}}\) (tanθ = \(\large{\frac{\sinθ}{\cosθ}}\) だから)
∴ T = \(\large{\frac{mg}{2\tanθ}}\)
(別解)
①式を導く方法はもう一つあります。
力のモーメントの大きさを求める考え方は、
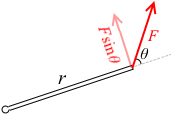 このようなものと、
このようなものと、
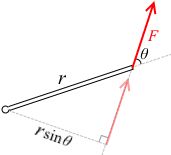 作用線に沿って移動して考えるこのようなものと、
作用線に沿って移動して考えるこのようなものと、
2通りあります。どちらも M = Frsinθ で同じです。
本問においても、力を作用線に沿って移動して力のモーメントを求めることができます。
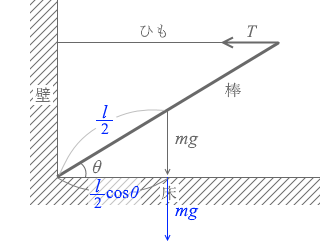 重力 mg を左図のように移動しますと、腕の長さは \(\large{\frac{l}{2}}\)cosθ であり、力のモーメントは
重力 mg を左図のように移動しますと、腕の長さは \(\large{\frac{l}{2}}\)cosθ であり、力のモーメントは
mg × \(\large{\frac{l}{2}}\)cosθ
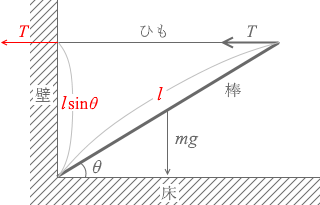 張力 T を左図のように移動しますと、腕の長さは lsinθ であり、力のモーメントは
張力 T を左図のように移動しますと、腕の長さは lsinθ であり、力のモーメントは
T × lsinθ
この2つの力のモーメントがつり合っているのだから、
mg × \(\large{\frac{l}{2}}\)cosθ = T × lsinθ
これは上の①式と同じです。
(余談)
T = \(\large{\frac{mg}{2\tanθ}}\) を解釈してみますと、角度 θ が大きいときは張力 T は小さく、角度 θ が小さいときは張力 T が大きい、といえます。
また、①式より、mgcosθ の大きさは Tsinθ の2倍であると分かります。