一些建议 小刺 2026/02/13(Fri) 22:33 No.850
内容做的非常不错!就是是否考虑添加一些习题之类的来辅助学习呢?
物理は相対性だけではない。 次郎 2026/01/07(Wed) 03:38 No.849
この世には、相対性原理しかないと思っていたら、大間違いで、
実は絶対性原理が正しく、相対性原理は完璧に間違いであった。
詳しくはこのサイトを見れば理解できる。
http://www3.ezbbs.net/19/1112/
実は絶対性原理が正しく、相対性原理は完璧に間違いであった。
詳しくはこのサイトを見れば理解できる。
http://www3.ezbbs.net/19/1112/
単振り子の復元力 タカ 2025/10/22(Wed) 22:52 No.847
単振り子のページの内容についての質問です。
「微小振動の単振り子の復元力」の解説中で、張力 S と重力 mg の合力が mgsinθ というわけではない とありますが、なぜでしょうか?
アスタリスクの補足を読んでもよく分かりませんでした。
「微小振動の単振り子の復元力」の解説中で、張力 S と重力 mg の合力が mgsinθ というわけではない とありますが、なぜでしょうか?
アスタリスクの補足を読んでもよく分かりませんでした。
Re: 単振り子の復元力
ろっとん 2025/10/23(Thu) 21:59 No.848
張力Sって少し大き目なんですよ。遠心力(=反心力)にも対抗しなければならないので。
これはちょっと難しいことなので理解できなかったらもう一度コメントください。
当該ページの私の説明もイマイチわかりにくいですね。。どうしよう。。。
これはちょっと難しいことなので理解できなかったらもう一度コメントください。
当該ページの私の説明もイマイチわかりにくいですね。。どうしよう。。。
自己インダクタンス ゔぁ 2025/10/11(Sat) 11:20 No.845
こんにちは。物理の復習にいつも使わせてもらっています。
1点、自己インダクタンスのページの記述について、気になった箇所がありましたのでお伝えさせてください。
自己インダクタンスとは
(省略)
また、L = μn2lS でありますので、透磁率の大きい物質が挿入されていて、巻きの密度が高くて、""長さが長く""て、断面積が大きいコイルの方が、その能力が高いといえます。自己インダクタンスはコイルの形状からくる性能を表しているともいえます。
長さが""長く""の箇所について""短く""が正しいと思われます。勘違いであったらすみません。よろしくお願いいたします。
1点、自己インダクタンスのページの記述について、気になった箇所がありましたのでお伝えさせてください。
自己インダクタンスとは
(省略)
また、L = μn2lS でありますので、透磁率の大きい物質が挿入されていて、巻きの密度が高くて、""長さが長く""て、断面積が大きいコイルの方が、その能力が高いといえます。自己インダクタンスはコイルの形状からくる性能を表しているともいえます。
長さが""長く""の箇所について""短く""が正しいと思われます。勘違いであったらすみません。よろしくお願いいたします。
Re: 自己インダクタンス
ろっとん 2025/10/14(Tue) 02:58 No.846
ん?どういうことでしょう?
No.840の画像追加 ななし 2025/09/03(Wed) 18:11 No.841
Re: No.840の画像追加
ろっとん 2025/09/04(Thu) 21:53 No.843
なんででしょうかね。
ななしさんの赤矢印の向きは掲載ページのものとほぼ同じなので簡単に比較して確かめられそうですが。
単純ミスではないですか?
ななしさんの赤矢印の向きは掲載ページのものとほぼ同じなので簡単に比較して確かめられそうですが。
単純ミスではないですか?
Re: No.840の画像追加
ななし 2025/09/05(Fri) 20:58 No.844
管理人様
ご返答ありがとうございます!
計算しなおしてみます。
お忙しいのに有難うございました。
ご返答ありがとうございます!
計算しなおしてみます。
お忙しいのに有難うございました。
キルヒホッフの解法について ななし 2025/09/03(Wed) 18:05 No.840
いつもこちらのサイトを拝見しており、大変助かっております。
高校物理が選択式で、一からこちらのサイトとテキストで勉強しているのですが、
キルヒホッフの法則を用いた回路の計算について質問です。
掲載ページで例題が1つあるのですが、その解法で疑問点があり
質問いたします。
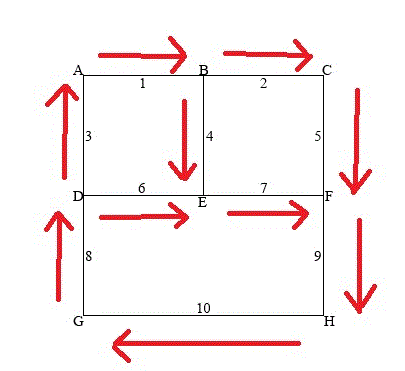
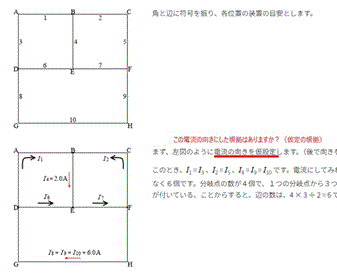
添付の画像をご確認ください。
①仮の電流の向きをそのように仮定した理由を教えてください。
②自分では、添付の赤矢印のように考えたのですが、全然計算があいません。
どうぞご教示のほどお願いいたします。
高校物理が選択式で、一からこちらのサイトとテキストで勉強しているのですが、
キルヒホッフの法則を用いた回路の計算について質問です。
掲載ページで例題が1つあるのですが、その解法で疑問点があり
質問いたします。
添付の画像をご確認ください。
①仮の電流の向きをそのように仮定した理由を教えてください。
②自分では、添付の赤矢印のように考えたのですが、全然計算があいません。
どうぞご教示のほどお願いいたします。
Re: キルヒホッフの解法について
ろっとん 2025/09/04(Thu) 21:46 No.842
仮定した理由はありません。
誤りの報告 shinji 2025/08/28(Thu) 18:02 No.838
大変参考になるサイトの運営を有難うございます。
解答に誤りが見つかりましたので、ご報告させて頂きます。
波動-固有振動-qH18B-問4で、解答がf3=132000 [Hz]となっていますが、
1320 [Hz]ではないかと思いましたのでお知らせ致します。
引き続き貴サイトのご発展を希望しております。
解答に誤りが見つかりましたので、ご報告させて頂きます。
波動-固有振動-qH18B-問4で、解答がf3=132000 [Hz]となっていますが、
1320 [Hz]ではないかと思いましたのでお知らせ致します。
引き続き貴サイトのご発展を希望しております。
Re: 誤りの報告
ろっとん 2025/08/31(Sun) 01:50 No.839
ありがとうございます。大変助かります。すぐ直します。
摩擦力のページについて 松橋 2025/06/07(Sat) 14:28 No.828
摩擦力についてのページ,摩擦力の式の項で,「摩擦力をFとしますと,F=μNで表せます」とありますが,「静止摩擦力の最大値がμNである」の間違いではないでしょうか。ご確認よろしくお願いします。
Re: 摩擦力のページについて
ろっとん 2025/06/08(Sun) 23:31 No.830
そうですね。かっこ付きで「動摩擦力の場合」と書いておくことにします。ご指摘ありがとうございます。
今年受験生 おき 2025/05/06(Tue) 14:31 No.826
私はものすごく論理的思考で、なぜ?といつも思ってしまいます。普通の人が気にもとめないような細かなところまで気になってしまいます。学校の物理の先生はとてもいい先生でものすごくわかりやすく、理由もきちんと説明してくださるのですが、一人で勉強しているとすぐにまた疑問が出てきてしまいます。しかし、このサイトに出会って、とても勉強が捗るようになりました!!私の疑問解消の手助けをいつもしてもらってます。特に動く図がわかりやすいです!もう受験まで1年きりましたが、これからも沢山使わせてもらいます!!
Re: 今年受験生
ろっとん 2025/05/06(Tue) 23:58 No.827
私も細かいところが気になってしまう性格です。でもそれでいいと思います。うやむやのままわかったような気になるより、とことん理由を突き詰めるほうがいいと思います。もちろん世の中はわからないことばかりで諦めなければならないことが多いですが。
いい先生に巡り合えたのはラッキーですね。私も高校時代にいい先生に出会えました。「仕事_補足」項で「ゆっくり」について解説しましたが、これはその先生が何度も繰り返し説明してくれたものです。物理において案外重要な概念です。
私もいい影響を与えられるように解説を改良していきますので今後もよろしくお願いします。
いい先生に巡り合えたのはラッキーですね。私も高校時代にいい先生に出会えました。「仕事_補足」項で「ゆっくり」について解説しましたが、これはその先生が何度も繰り返し説明してくれたものです。物理において案外重要な概念です。
私もいい影響を与えられるように解説を改良していきますので今後もよろしくお願いします。
お世話になりました うるる 2025/04/15(Tue) 21:24 No.822
受験を無事終え、新生活にも少しは慣れてきた頃なので戻って参りました`・ω・)ゞ
受験期の春ごろは物理が一番出来が悪く、どうしたもんかね…´・ω・`という状況でした。
夏になってたまたまこのサイトに出会い、ゆっくり読み込むことで知識が定着していき、その感覚が嬉しくてばりばりやったおかげで成績は右肩上がりになりました> <
説明は私好みでわかりやすいかつ面白く、痒いところにも手が届きますし、GIFも沢山差し込まれていてすごく見やすかったです;;
このサイトのおかげで物理がもっと好きになり、学校の最後の定期テストでは満点をとることができました`ω´このサイトを何度も読んで猛勉強しましたからね!
結局第二志望に行くことにはなりましたが、成績をぐっと伸ばせたことは自信に繋がっています¯ω¯『ここから先は大学で勉強してください』の部分がこれから勉強できるのが楽しみです。本当にありがとうございました!
p.s.未だにお守りがわり(?)にこのサイトのタブを開いたままにしています。きっとまだまだお世話になります。
受験期の春ごろは物理が一番出来が悪く、どうしたもんかね…´・ω・`という状況でした。
夏になってたまたまこのサイトに出会い、ゆっくり読み込むことで知識が定着していき、その感覚が嬉しくてばりばりやったおかげで成績は右肩上がりになりました> <
説明は私好みでわかりやすいかつ面白く、痒いところにも手が届きますし、GIFも沢山差し込まれていてすごく見やすかったです;;
このサイトのおかげで物理がもっと好きになり、学校の最後の定期テストでは満点をとることができました`ω´このサイトを何度も読んで猛勉強しましたからね!
結局第二志望に行くことにはなりましたが、成績をぐっと伸ばせたことは自信に繋がっています¯ω¯『ここから先は大学で勉強してください』の部分がこれから勉強できるのが楽しみです。本当にありがとうございました!
p.s.未だにお守りがわり(?)にこのサイトのタブを開いたままにしています。きっとまだまだお世話になります。
Re: お世話になりました
ろっとん 2025/04/16(Wed) 19:10 No.823
コメントありがとうございます。
苦手だった物理を好きになってくれたのは本当にうれしいです。本サイトは受験対策も意識してますが、本当の目的は物理の楽しさを伝えることです。それが伝わったのが最もうれしいです。
大学の授業、教科書はわかりにくくて面食らうと思いますが楽しみながらなんとか頑張ってください。
苦手だった物理を好きになってくれたのは本当にうれしいです。本サイトは受験対策も意識してますが、本当の目的は物理の楽しさを伝えることです。それが伝わったのが最もうれしいです。
大学の授業、教科書はわかりにくくて面食らうと思いますが楽しみながらなんとか頑張ってください。