電磁誘導

ファラデーの電磁誘導の法則

『レンツの法則』項において説明した電磁誘導について、その誘導起電力の大きさを本項で説明します。

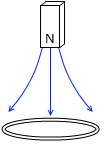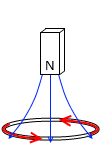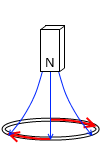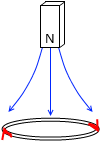
ファラデーの実験によれば、
N巻きのコイルを貫く磁束が、Δt [s] 間に ΔΦ [Wb] だけ変化するとき、コイルに発生する誘導起電力 V [V] は、

となります。コイルが 1巻きであれば、

　　　　V = - \(\large{\frac{ΔΦ}{Δt}}\)

です。

この法則の原理については、『電磁誘導とローレンツ力』項と『磁場を横切る導線』項をお読みください。

-（マイナス）はレンツの法則

-（マイナス）が付くのは、

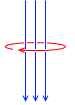たとえば、鉛直下向きの磁束が増加したときに発生する誘導起電力の正の向きが右回りと決められているからです。（実際には左回りの誘導起電力が発生するのですが、とりあえず、正と負の向きを決めるときに、磁束が鉛直下向きのときは、右回りが正、と決める、ということです。）

物理法則の向きは（世の中のほとんどの物の向きもそうですが）右ねじにのっとった向きに決められることが多いです。

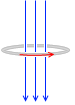下向きの磁束が増えた場合というのは、レンツの法則により、上向きの磁束をつくるような電流がコイルに流れます。その電流の向きは左回りです。これは負の向きです。ですので - が付きます。

つまり、- はレンツの法則を表現しているといえます。

- が付くことを忘れてしまっても、レンツの法則さえ頭に入っていれば大丈夫です。試験問題を解くことはできます。

速く動かす方が誘導起電力が大きくなる

\(\large{\frac{ΔΦ}{Δt}}\) というのは磁束 Φ の変化がどれだけ急であるかを示す量です。

微分積分に慣れている方は理解できると思いますが、これは変位に対する速度のようなものです。

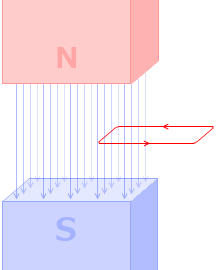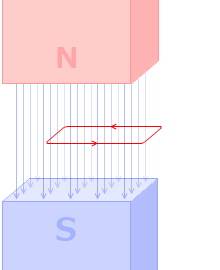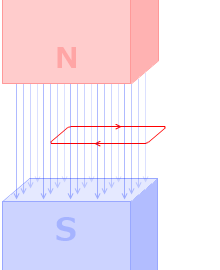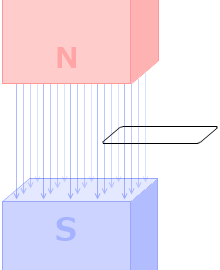コイルを貫く磁束の数がゆっくり変化するよりも、

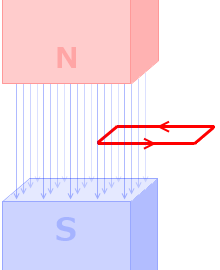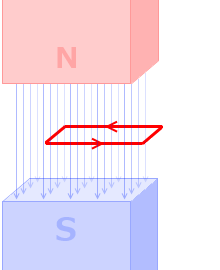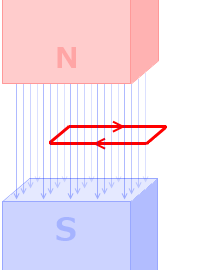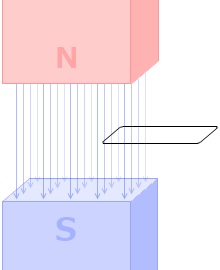急激に変化する方が、発生する誘導起電力 V は大きくなります。

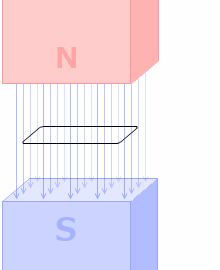動きを止めれば、誘導起電力は 0 になります。

複数巻き

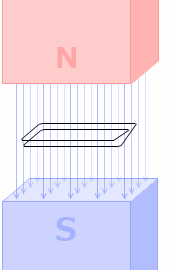コイルは 1巻きよりも、

2巻きの方が誘導起電力が大きくなります。2倍になります。でも導線も2本になるわけですから、1本当たりの電流の大きさは変わりません。

コイルを磁束の方向に動かしても誘導起電力は発生しない

磁場が一様な場合、コイル（あるいは磁石）を磁束と同じ方向に動かしても、誘導起電力は発生しません。コイルを貫く磁束の本数が変わらないからです。

ですから、もし磁石から出る磁束がこのような形であったら『レンツの法則』項で示したコイルには電流は発生しないことになります。

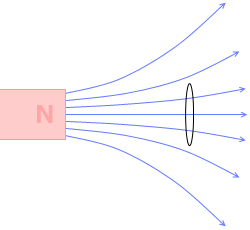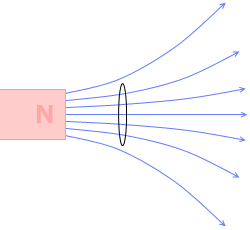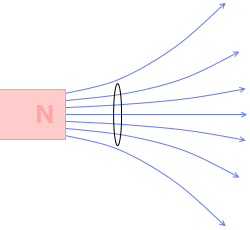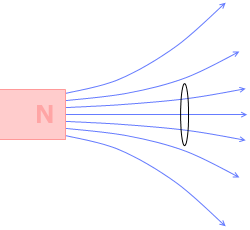磁石から出る磁束がこのような形であるからこそ、磁石とコイルの距離が変わることによって、コイルを貫く磁束の本数が変わり、電磁誘導が起こるのです。

（左のアニメーションは目の錯覚で円の大きさが変わるように見えてしまいます、、、）

磁場にすっぽり覆われた中で角度を変えずに動かしても誘導起電力は発生しない

一様な磁場にすっぽり覆われる状態で、コイルの角度を変えずにコイルを動かしても、誘導起電力は発生しません。コイルを貫く磁束の本数が変わらないからです。

磁場の中でコイルの角度を変えると誘導起電力が発生する

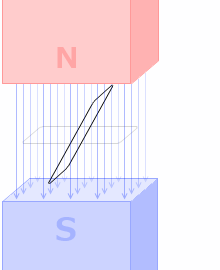コイルが斜めになると、コイルを貫く磁束の本数が少なくなります。

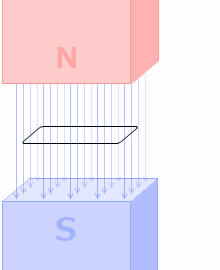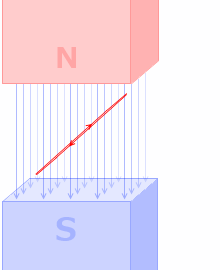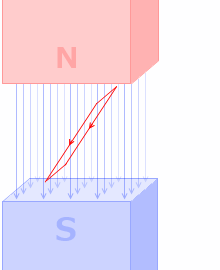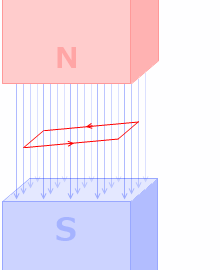ですので、磁場の中でコイルの角度を変えると誘導起電力が発生します。発電機の原理です。