磁束密度
磁束密度
磁場の強さ H [A/m] に透磁率 μ [N/A2] を掛けたものを磁束密度といいます。B で表します*この量記号 B の語源は分かりません。
ビオ・サバール Biot-Savart から、という噂もあります。
閉じる。
B = μH
です。
磁場の強さはベクトルであり、磁束密度は磁場の強さに透磁率(透磁率は単なる数値)を掛けたものだからベクトルです*ベクトルにスカラーを掛けたものはベクトルです。
閉じる。ベクトルであることを意識して式をあらためて書き直すと、以下のようになります。
磁束密度
\(\vec{B}\) = μ\(\vec{H}\)
磁束密度の単位
上式の単位を書き出してみると、
B = μ [N/A2] × H [A/m]
B = [N/A2] × [A/m]
B = [N/A⋅m]
です。磁束密度 B の単位は [N/A⋅m] ニュートン毎アンペア毎メートル です。また、[A/m] = [N/Wb] でありますから、
[N/A⋅m] = \(\large{\frac{\rm[N]}{\rm[A\cdot m]}}\) = \(\large{\frac{\rm[N/m^2]}{\rm[A\cdot m/m^2]}}\) = \(\large{\frac{\rm[N/m^2]}{\rm[A/m]}}\) = \(\large{\frac{\rm[N/m^2]}{\rm[N/Wb]}}\) = \(\large{\frac{\rm[1/m^2]}{\rm[1/Wb]}}\) = \(\large{\frac{\rm[Wb]}{\rm[m^2]}}\) = [Wb/m2](ウェーバ毎平方メートル)
です。この単位は [T] テスラ とも書き表されます*19世紀のオーストリアの発明家 ニコラ⋅テスラ Nikola Tesla より。
閉じる。
要するに、磁束密度 B の単位は [N/A⋅m] または [Wb/m2] または [T] です。
磁束
磁束密度に面積を掛けたものを磁束といいます。Φ(ファイ)で表します*ギリシア文字です。大文字です。Φ の小文字は φ です。
なぜこの文字が磁束の量記号に使われてるのかについては分かりません。
閉じる。磁束は大きさだけを表し、方向はありません。スカラーです。磁束密度には方向があります。磁束密度と面積を掛けるときはお互いに直交していなければなりません。(あるいは直交している成分だけを掛け合わせなければなりません。『斜めに横切る場合』参照)。圧力と同じ考え方です。
磁束密度が B [Wb/m2] の一様な磁場において、それに垂直な面積 S [m2] の部分の磁束は、
磁束
Φ = BS
となります。
磁束の単位
磁束の単位は [Wb] ウェーバ です。B の単位が [Wb/m2] で S の単位が [m2] なので、それらを掛け合わせた Φ の単位は [Wb] です。
(磁束密度が 3Wb/m2 の磁場の中でそれに垂直な 5m2 の面積の部分の磁束は 15Wb です。10m2 なら 30Wb です。)
この単位は磁気量の単位でもあります。
磁束密度と磁束の違い
下記A面の面積はB面の2倍であるとします。
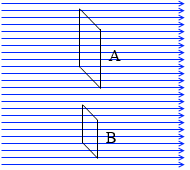 A面とB面の磁束密度は同じです。
A面とB面の磁束密度は同じです。
A面の磁束はB面の2倍です。
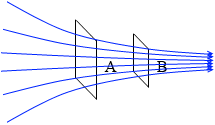 A面の磁束密度はB面の半分です。
A面の磁束密度はB面の半分です。
A面とB面の磁束は同じです。
(本当は3次元で表現しなければなりません。上のイラストの磁束線は2次元で表現されています。)
式の書き換え
B = μH の関係を F = μIHlsinθ 式の μH部分に当てはめると、以下のようになります。
F = IBlsinθ
これまでに出てきた磁気力に関する式をまとめてみます。
F = mH …… 磁極の強さを含む式。電流に無関係の式。
F = IBlsinθ …… F = μIHlsinθ の μH部分を B に置き換えた式。電流が関係する式。f = qvBsinθ と同等の式。
また、B = μH 式に『電流がつくる磁場』項で示した各電流がつくる磁場の式を代入すると、磁束密度の式が得られます。
直線電流がつくる磁束密度 B = \(\large{\frac{μI}{2\pi r}}\) ( ← H = \(\large{\frac{I}{2\pi r}}\) )
円形電流がつくる磁束密度 B = \(\large{\frac{μI}{2r}}\) ( ← H = \(\large{\frac{I}{2r}}\) )
ソレノイドがつくる磁束密度 B = μnI ( ← H = nI )
B と H の違い
透磁率 μ と真空の透磁率 μ0 と比透磁率 μr の3つは、
μr = \(\large{\frac{μ}{μ_0}}\)
という関係がありますから、
μ = μr μ0
です。これを \(\vec{B}\) = μ\(\vec{H}\) に代入すると、
\(\vec{B}\) = μr μ0\(\vec{H}\)
です。
この式の μr と μ0 は単なる数値(スカラー)で \(\vec{B}\) と \(\vec{H}\) だけがベクトルです。ですので \(\vec{B}\) と \(\vec{H}\) の向きは平行です*たとえば \(\vec{B}\) が西向きならば、それを何倍かしたとしても \(\vec{H}\) は西向きです。
ベクトルにスカラーを掛けても向きは元のままです。ベクトルには「大きさ」と「向き」の2つの要素があります。ベクトルにスカラーを掛けると「大きさ」だけが変化し、「向き」は変わりません。
閉じる。
もし今、真空中での話だとすると μr = 1 であり、式は \(\vec{B}\) = μ0\(\vec{H}\) となります。
この μ0(真空の透磁率)は 4π×10-7 という定数で、これは F = μIHlsinθ という式を成り立たせるための便宜上の数値です。単位を揃えるためのものです。
ですから \(\vec{B}\) = μ0\(\vec{H}\) という式は、\(\vec{B}\) と \(\vec{H}\) は本質的に同じものである、ということを示しているといえます。
磁場という言葉
「磁場」という言葉は \(\vec{H}\)(磁場の強さ)のことを指したり、\(\vec{B}\)(磁束密度)のことを指したりします。E-B対応とE-H対応という問題もあります。非常にややこしいです。*ちなみに「磁場」という言葉と「磁界」という言葉はまったく同じ意味です。
閉じる
磁力線と磁束線
 \(\vec{H}\) を図で表すときは磁力線で表現しましたが、\(\vec{B}\) を図で表すときは磁束線というものを使います。
\(\vec{H}\) を図で表すときは磁力線で表現しましたが、\(\vec{B}\) を図で表すときは磁束線というものを使います。
\(\vec{B}\) = μ0\(\vec{H}\) における μ0 は 4π×10-7(≒0.00000126) というとても小さい数値なので、磁束線の方が本数が少なくなり、磁力線と磁束線を同時に描くとそのイメージは左図のようになります。(通常、磁力線と磁束線を同時に描くことはありません。2つを明確に区別しないことも多いです)。磁束線は磁力線を「束」にしたものと考えられます。
もし今、真空中ではない話だとすると、式は \(\vec{B}\) = μr μ0\(\vec{H}\) であり、μr というのは比透磁率であり、これは便宜上の数値というわけではなく物質によって変わる値です。『磁化』において、物質には強磁性体と常磁性体と反磁性体の3種があると説明しましたが、常磁性体の比透磁率は 1.000001 などという値で、反磁性体の比透磁率は 0.99999 などという値であるので、真空の場合とほとんど変わりません。しかし、強磁性体であるたとえば鉄の比透磁率は 5000 くらいですので、磁束密度 \(\vec{B}\) の値はとても大きくなります。
 磁場の中に鉄を置いたときの磁束線のイメージは左図のようになります。
磁場の中に鉄を置いたときの磁束線のイメージは左図のようになります。
磁化の概念
『磁化』において、物質中の電子のスピンの方向が揃うことが磁化である、と説明しましたが、
 電子のスピンというのは、これは微小な円形電流であるといえます。
電子のスピンというのは、これは微小な円形電流であるといえます。
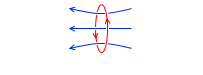 この微小円電流は磁場をつくります。
この微小円電流は磁場をつくります。
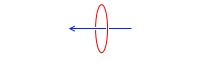 これを左図のように描くことにします。
これを左図のように描くことにします。
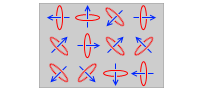 磁化されてない物質は、微小円電流の向きがバラバラで、トータルとして磁場が相殺されて 0 になっています。
磁化されてない物質は、微小円電流の向きがバラバラで、トータルとして磁場が相殺されて 0 になっています。
 鉄などの強磁性体が磁場の中に置かれると、微小円電流の向きが揃い、磁束線が増え、磁場が強くなります。これが磁化です。
鉄などの強磁性体が磁場の中に置かれると、微小円電流の向きが揃い、磁束線が増え、磁場が強くなります。これが磁化です。
鉄心
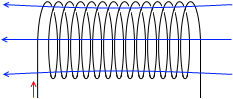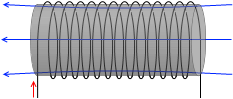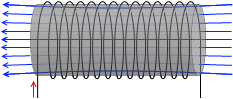 ソレノイドに鉄心(鉄芯)を挿入すると磁場が大幅に増加します。電磁石です。普通の磁石(永久磁石)より強い磁場を作り出すことができます。
ソレノイドに鉄心(鉄芯)を挿入すると磁場が大幅に増加します。電磁石です。普通の磁石(永久磁石)より強い磁場を作り出すことができます。
上で説明しましたがソレノイドがつくる磁束密度は B = μnI です。μ = μrμ0 (これも上で説明しました)を代入すると、
B = μrμ0nI
です。ソレノイドに何も挿入してない(空気 μr≒1)ときは
B = μ0nI
ですが、鉄心(鉄 μr≒5000)を挿入したとき(コイル内に隙間なく満たしたと仮定したとき)は
B = 5000μ0nI
です。磁束密度が大幅に増加します。*5000μ0nI という計算が成り立つのはあくまでも理論上の話です。無限長のソレノイドでの話です。
閉じる