電磁誘導をローレンツ力から考える
電磁誘導が起こる仕組みをローレンツ力から考える
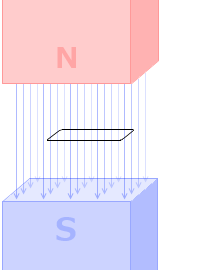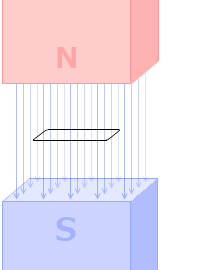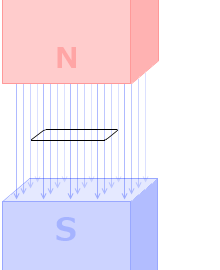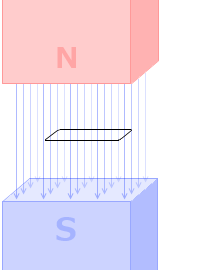
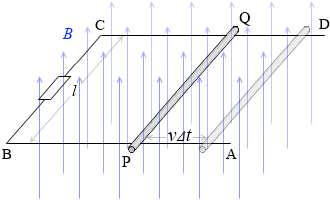『磁場を横切る導線』項で、このような回路における電磁誘導について説明しましたが、
このときの導体棒の中の自由電子に着目してみます。
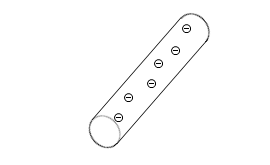導体棒には無数の自由電子が存在しています。
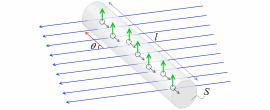
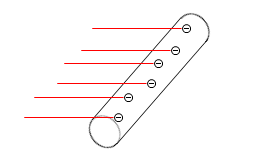導体棒を右に引っ張ると、その自由電子たちが動くことになります。たとえ導体棒の中で止まっていたとしても導体棒全体が動くのでその中にいる自由電子も動いてしまいます。
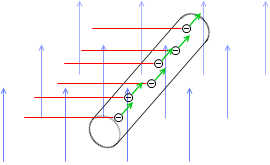そして、磁場の中で動く荷電粒子はローレンツ力を受けます。
その向きはフレミングの左手の法則によります。左図の緑矢印のような向きです。フレミングの左手の法則の「電」は自由電子の電ではなく電流の電であり、電流の向きは自由電子の向きと逆であることに注意してください。
（また、この話は『ローレンツ力』項の左図の話とは違うことに気をつけてください。左図は、もともと電流が流れている導線を磁場の中に置いた場合の話です。電子が導線の長さ方向に動いている場合の話です。本項の話は、まだ電流が流れていない導線の話です。電子を導線と垂直な方向へ力づくで動かした場合の話です。どちらもローレンツ力が原因で起こる現象ではあります。）
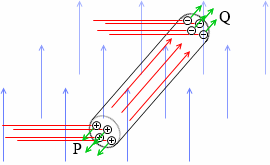
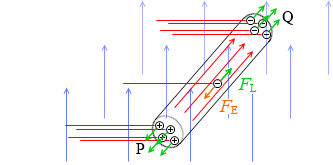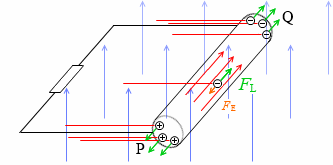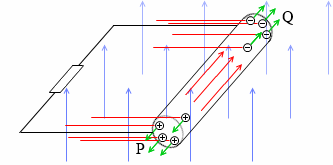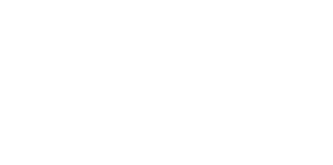
ローレンツ力がP→Qの方向にはたらくので自由電子がQに集まります。
Qは負に帯電し、Pは自由電子が少なくなるので正に帯電します（正電荷がPに集まるとも考えられます）。
すると今度は、P→Qの向きに電場（電位差）が生じます。（電場の方向はP→Q。QよりPの方が電位が高い。電流の方向はQ→P。とてもややこしいです。）
Qの負電荷、Pの正電荷が増えていってこの電場が大きくなっていくと、自由電子をPの方向へ持って行こうとする静電気力が大きくなっていきます。負電荷である自由電子がPの正電荷に引き寄せられるということです。
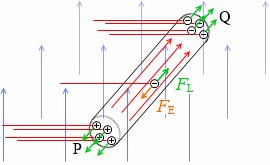やがて、Q方向へのローレンツ力とP方向への静電気力がつり合います。ホール効果と同じ原理です。
磁束密度を B [T] 、導体棒の速さを v [m/s] とすると、1つの自由電子＊電荷量を -e [C] とします。大きさだけをいえば e [C] です。
閉じるにはたらくローレンツ力 FL [N] の大きさは、
FL = evB
P→Qの方向に生じる電場を E [V/m] とすると、1つの自由電子にはたらく静電気力の大きさ FE [N] は、
FE = eE
この2力がつり合うのだから、
FE = FL
∴ eE = evB
∴ E = vB
となります。磁束密度 B の磁場の中で導体棒を v で動かすとその内部に E = vB の電場が生じるということです。
PQの長さを l [m] としますと、PQ間の電位差 V [V] は、
V = (電場) × (距離) = E × l = vBl
であり、これは、『磁場を横切る導線』項で示した、磁場を横切る導線に生じる誘導起電力 V = vBl に一致します。
電磁誘導というものは、
磁場の中で導線を動かす → ローレンツ力により電荷の分布が偏る → 電場が発生する → その電場の大きさはローレンツ力の大きさ、つまり v や B の大きさにに比例する → 電場に距離を掛けると電位差（起電力）になる → 誘導起電力の大きさは V = vBl である
というものです。
磁場の中を動く導体棒は電池
磁場を横切る導体棒には誘導起電力が生じるので、これは電池である、ともみなせます。
回路につなぐと、
Qから - の電荷が押し出され（これはQに + の電荷が入ってくるという意味でもあります）、Pから + の電荷が押し出され（Pに - が入ってくる）、上で示した式 FE = FL が FE < FL となり、
ローレンツ力が新たに - 電荷をQに、+ 電荷をPに追いやり、FE = FL となり、
Qから - 電荷が、Pから + 電荷が、押し出され、FE < FL となり、
ローレンツ力が新たに…、
ということを繰り返します。
この間、PQの電位差が V = vBl に保たれるわけです。（上図で例えれば、- の個数や + の個数が保たれるということです）。この導体棒は vBl [V] の電池に例えることができます。（一般に売られている乾電池は 1.5V です）。
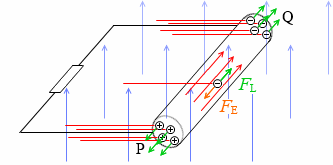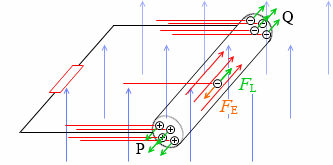この導体棒に抵抗をつなげばジュール熱が発生しますし、
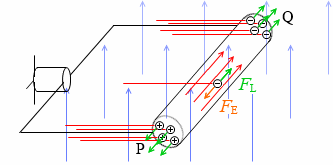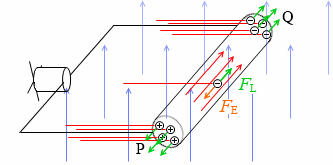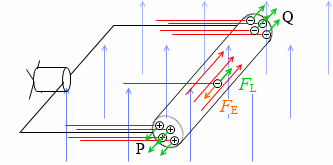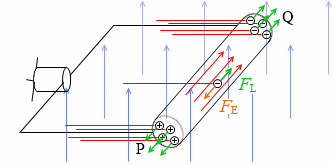プロペラ付きモーターをつなげばプロペラが回ります。
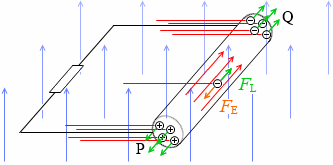ただし、回路全体が磁場の中にある場合はうまくいきません。＊
これはもちろん右辺の導体棒だけがスライドしながら動くというような話ではありません。そうならわざわざ取り上げる話ではありません。これは回路全体が動くという話です。
閉じる
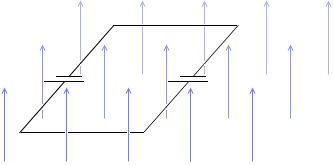これは起電力が逆向きに2つ付いてるようなものです。左辺の導線にも誘導起電力が発生してしまいます。